 La funzione di elevamento al quadrato
La funzione di elevamento al quadrato
E' stato utilizzato il package ComplexMapPlot di Theodore W. Gray e Jerry Glynn, tratto dal volume
Exploring Mathematics with Mathematica
Addison-Wesley, 1991.
 La funzione di elevamento al quadrato
La funzione di elevamento al quadrato
Alcuni segmenti orizzontali nel primo quadrante:
Input :=
ComplexMapPlot[z^2, z, HorizontalLines[{{0,1},{0,1}},
PlotPoints -> 7], PlotRange -> All];
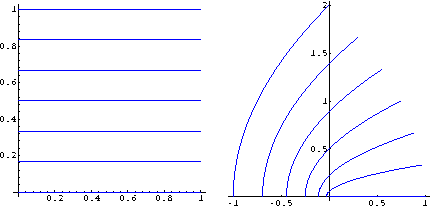
Alcuni segmenti orizzontali nel quarto quadrante:
Input :=
ComplexMapPlot[z^2, z, HorizontalLines[{{0,1},{-1,0}},
PlotPoints->7], PlotRange->All];
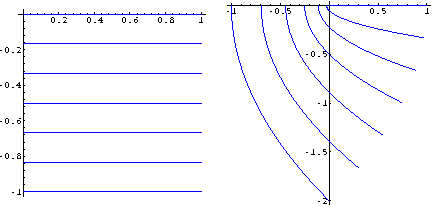
Alcuni segmenti verticali nel primo e quarto quadrante:
Input :=
ComplexMapPlot[z^2, z, VerticalLines[{{0,1},{-1,1}},
PlotPoints->7], PlotRange->All];
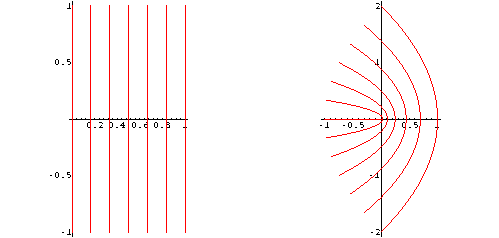
L'unione delle tre famiglie di segmenti precedenti:
Input :=
ComplexMapPlot[z^2, z, RectangularGrid[{{0,1},{-1,1}},
PlotPoints->7], PlotRange->All];
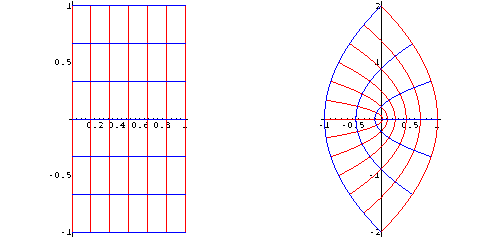
 La funzione radice quadrata principale
La funzione radice quadrata principale
Tutti i punti del piano complesso hanno immagini con parte reale non negativa.
Input :=
ComplexMapPlot[Sqrt[z], z,
RectangularGrid[{{-2,2},{-2,2}}],
Ticks -> {{-2., -1., 1., 2.}, Automatic}];
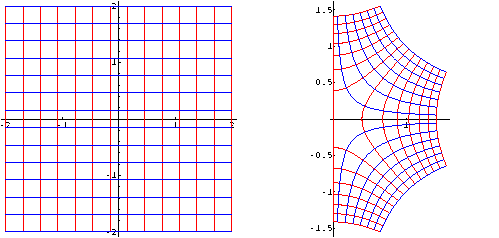
Input :=
ComplexMapPlot[Sqrt[z], z,
{Thickness[0.001], PolarGrid[{0,0},{0,2}]},
Ticks -> {{0.5, 1., 1.5}, Automatic}];

 La funzione z -> 1/z
La funzione z -> 1/z
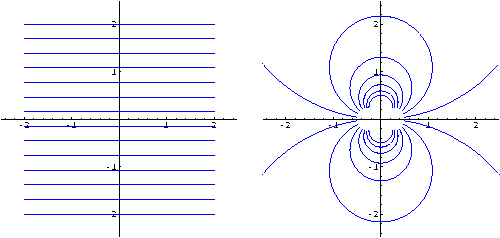
Le circonferenze hanno come immagini circonferenze (le rette sono casi limite di circonferenze).
Input :=
ComplexMapPlot[1/z, z, HorizontalLines[{{-2,2},{-2,2}}],
PlotRange->{{-2.5,2.5},{-2.5,2.5}}];
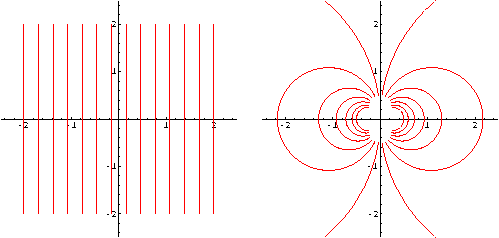
Input :=
ComplexMapPlot[1/z, z, VerticalLines[{{-2,2},{-2,2}}],
PlotRange->{{-2.5,2.5},{-2.5,2.5}}];
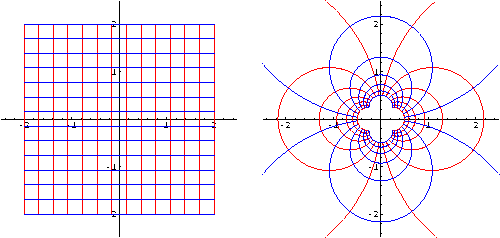
Input :=
ComplexMapPlot[1/z, z, RectangularGrid[{{-2,2},{-2,2}}],
PlotRange->{{-2.5,2.5},{-2.5,2.5}}];
Input :=
ComplexMapPlot[1/z, z,
{Thickness[0.001], PolarGrid[{0,0}, {0.1, 2}]}];
 La funzione esponenziale
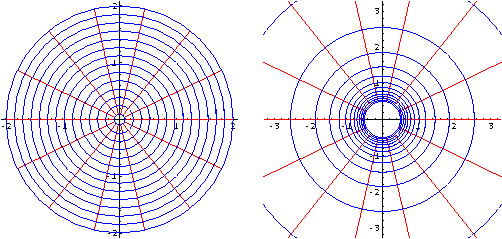
La funzione esponenziale
Segmenti paralleli all'asse reale hanno come immagini segmenti appartenenti a semirette uscenti dall'origine, segmenti paralleli all'asse immaginario hanno come immagini archi di circonferenza di centro l'origine:
Input :=
ComplexMapPlot[Exp[z], z,
RectangularGrid[{{-1,2},{-2,2}}],
PlotRange-> All];
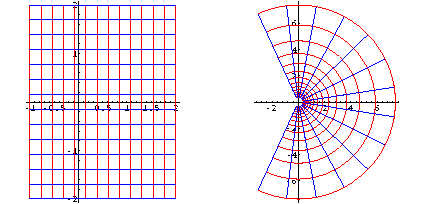
Segmenti paralleli all'asse immaginario aventi lunghezza 2 pi greco hanno come immagine un'intera circonferenza:
Input :=
ComplexMapPlot[Exp[z], z,
RectangularGrid[{{-2,2},{-Pi,Pi}}],
PlotRange-> All];
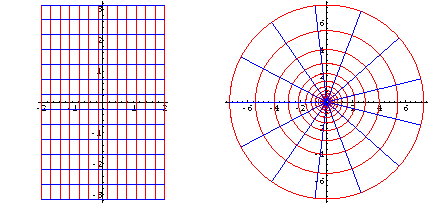
Le immagini di alcune circonferenze di centro l'origine e raggi non superiori a 2:
Input :=
ComplexMapPlot[Exp[z], z,
{Thickness[0.001], PolarGrid[{0,0}, 2]},
PlotRange-> All];
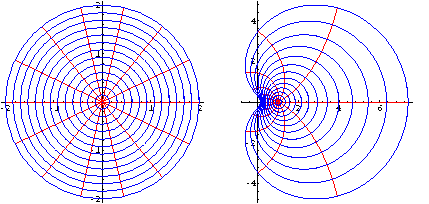
Le circonferenze di partenza sono tutte contenute nella striscia
- pigreco < Im z <= pigreco
in cui la funzione esponenziale è iniettiva. Dunque immagini di curve semplici chiuse sono ancora curve dello stesso tipo.
Costruiamo le immagini di circonferenze di centro l'origine e raggi che vanno da valori di poco inferiori a pigreco a valori di poco superiori:
Input :=
Table[
ParametricPlot[
{Re[Exp[(Pi+h) Exp[I t]]],
Im[Exp[(Pi+h) Exp[I t]]]},
{t, 0, 2Pi},
AspectRatio -> Automatic,
PlotPoints -> 60,
PlotRange -> {{-10,30}, {-22,22}},
Ticks -> {{-10,10,20,30}, {-20,-10,10,20}},
DisplayFunction -> Identity,
Prolog -> {RGBColor[1,0,0]},
Epilog -> {RGBColor[0,0,1],
Text["r = ", {6,10}, {-1,0}],
Text[N[Pi+h,4], {14,10},{-1,0}]}
],
{h, -0.3, 0.3, 0.1}
];
Input :=
Show[GraphicsArray[Partition[%, 3]],
GraphicsSpacing -> {0.3, 0.3}];
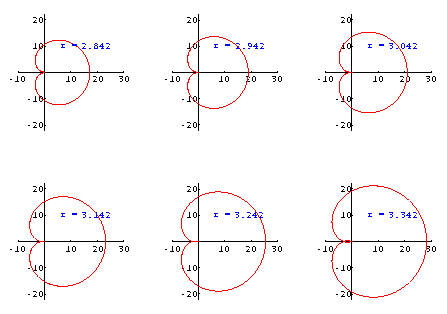
Per vedere meglio che cosa accade in prossimità dell'origine, mostriamo soltanto la finestra
-4 < Re z < 0.5, -0.5 < Im z < 0.5.
I grafici che seguono non sono monometrici.
Input :=
Table[
ParametricPlot[
{Re[Exp[(Pi+h) Exp[I t]]],
Im[Exp[(Pi+h) Exp[I t]]]},
{t, 0, 2Pi},
PlotPoints -> 60,
PlotRange -> {{-4., 0.5},{-0.5,0.5}},
DisplayFunction -> Identity,
Prolog -> {Thickness[0.015], RGBColor[1,0,0]},
Epilog -> {RGBColor[0,0,1],
Text["r = ", {-4,0.3}, {-1,0}],
Text[N[Pi+h,4], {-3.3,0.3},{-1,0}]}
],
{h, -0.2, 0.15, 0.05}
];
Input :=
Show[GraphicsArray[Partition[%, 2]],
GraphicsSpacing->{0.3, 0.1}];
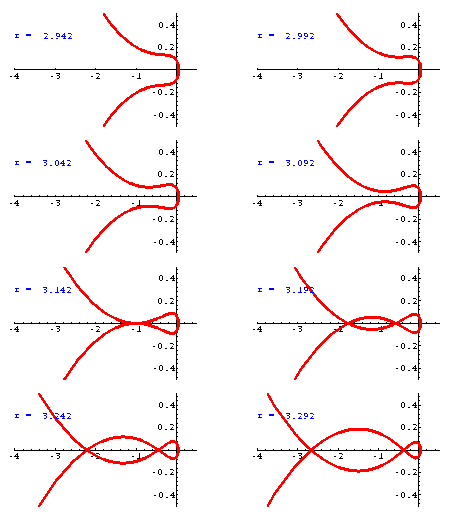
I grafici vanno esaminati dall'alto al basso, da sinistra a destra. Il grafico che mostra l'immagine della circonferenza di raggio pigreco e' quello a sinistra nella quarta riga. Il punto -1 è l'immagine comune dei punti
z = i pigreco, z = -i pigreco. Tutti i grafici mostrati incontrano il semiasse reale positivo nel punto di ascissa exp(-r).
Ripetiamo i grafici precedenti, mostrando soltanto l'immagine della semicirconferenza contenuta nel sempiano Re z < 0. Anche i grafici che seguono non sono monometrici.
Input :=
Table[
ParametricPlot[
{Re[Exp[(Pi+h) Exp[I t]]],
Im[Exp[(Pi+h) Exp[I t]]]},
{t, Pi/2, 3 Pi/2},
PlotPoints -> 60,
PlotRange -> {{-1.5, 0.5},{-0.5,0.5}},
Ticks -> {{-1.5,-1,-0.5,0.5},Automatic},
DisplayFunction -> Identity,
Prolog -> {Thickness[0.015], RGBColor[1,0,0]},
Epilog -> {RGBColor[0,0,1],
Text["r = ", {-1.5,0.3}, {-1,0}],
Text[N[Pi+h,4], {-1.2,0.3},{-1,0}]}
],
{h, -0.2, 0.15, 0.05}
];
Input :=
Show[GraphicsArray[Partition[%, 2]],
GraphicsSpacing->{0.3, 0.1}];
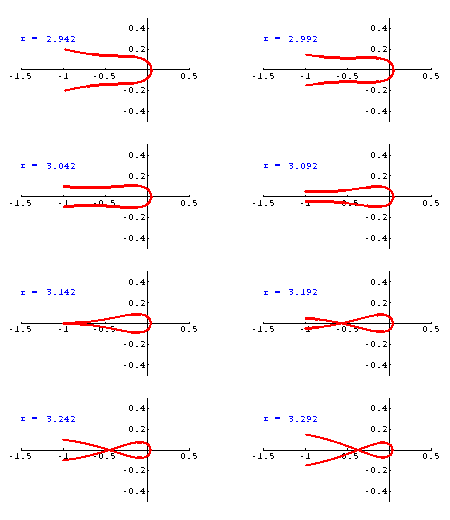
 La funzione logaritmo principale
La funzione logaritmo principale
Input :=
ComplexMapPlot[Log[z], z,
RectangularGrid[{{-2,2},{-2,2}}],
PlotRange-> All];
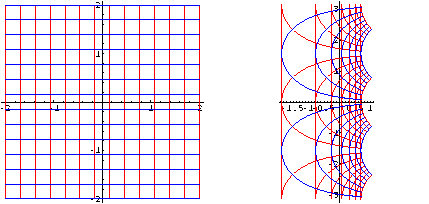
I segmenti "verticali" che compaiono nel grafico di destra sono ingannevoli: essi sono le immagini di "piccoli" segmenti che hanno un estremo immediatamente al disotto del semiasse reale negativo e l'altro estremo immediatamente al disopra dello stesso semiasse.
Più esattamente: essi sono i segmenti che congiungono le immagini degli estremi dei segmenti appena descritti. Tali segmenti attraversano il semiasse reale negativo che è luogo dei punti di discontinuità della funzione logaritmo principale.
Nel seguito vengono mostrati grafici relativi a segmenti "verticali" che non attraversano il semiasse reale negativo.
Per cominciare alcuni segmenti "orizzontali": se un punto si muove nel piano z da sinistra a destra (Re z crescente) il punto corrispondente si muove nel senso dell'avvicinamento all'asse reale.
Input :=
ComplexMapPlot[Log[z], z,
HorizontalLines[{{-2,2},{-2,2}}],
PlotRange-> All];
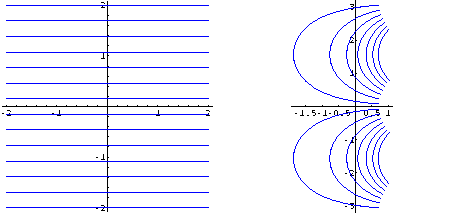
Alcuni segmenti verticali contenuti nel primo e secondo quadrante: se un punto si muove nel piano z dal basso all'alto (Im z crescente) il punto corrispondente si muove nel senso dell'avvicinamento alla retta di ordinata 1/2, immagine del semiasse immaginario positivo.
Input :=
ComplexMapPlot[Log[z], z,
VerticalLines[{{-2,2},{0,2}},
PlotPoints->13]];
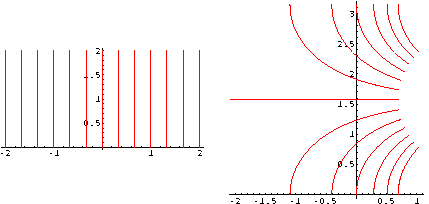
Alcuni segmenti verticali contenuti nel terzo e quarto quadrante: i secondi estremi sono un poco al disotto dell'asse reale.
Input :=
ComplexMapPlot[Log[z], z,
VerticalLines[{{-2,2},{-2,-0.01}},
PlotPoints -> 13]];
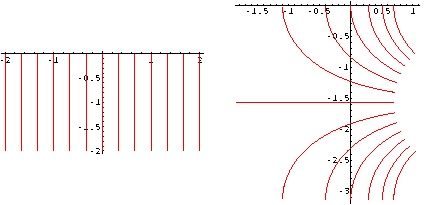
Input :=
ComplexMapPlot[Log[z], z,
{Thickness[0.001], PolarGrid[{0,0},{0.1,2}]},
PlotRange->All];
 La funzione seno
La funzione seno
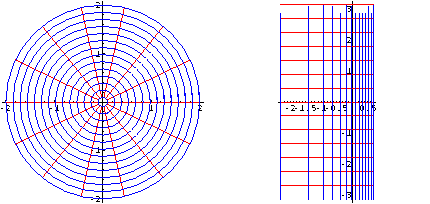
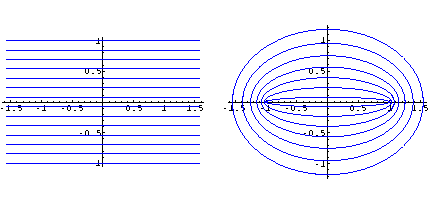
Segmenti parallali all'asse reale hanno come immagini archi di ellissi aventi i fuochi nei punti z1 = -1, z2 = 1; tali archi sono delle semiellissi se i segmenti originali hanno lunghezza pi greco.
Segmenti paralleli all'asse immaginario hanno come immagini archi di iperboli aventi i fuochi negli stessi punti delle ellissi.
Input :=
ComplexMapPlot[Sin[z], z,
{Thickness[0.001],
HorizontalLines[{{-Pi/2,Pi/2},{-1,1}}]}];
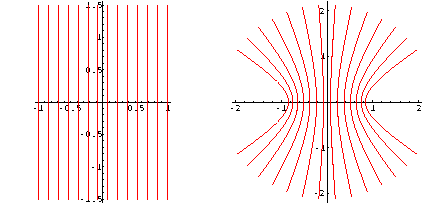
Input :=
ComplexMapPlot[Sin[z], z,
{Thickness[0.001],
VerticalLines[{{-1,1},{-1.5,1.5}}]},
PlotRange -> All];
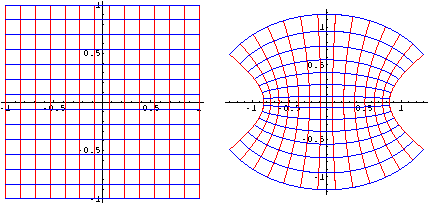
Input :=
ComplexMapPlot[Sin[z], z,
RectangularGrid[{{-1,1},{-1,1}}]];
 Grafici del tipo z -> | f(z)|
Grafici del tipo z -> | f(z)|
Input := z = x + I y;
 Funzione seno
Funzione seno
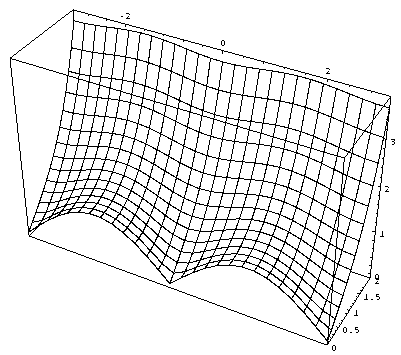
Input :=
Plot3D[Abs[Sin[z]], {x,-Pi, Pi}, {y, 0, 2},
Shading->False, PlotPoints ->{27, 15},
BoxRatios -> {2Pi, 2, 4}];
Input :=
Plot3D[Abs[Sin[z]], {x,-Pi, Pi}, {y,-2, 2},
Shading -> False, PlotPoints -> {27, 15},
BoxRatios -> {2Pi, 4, 4},
ViewPoint -> {3.3, -2.5, 2}];
 Funzione esponenziale
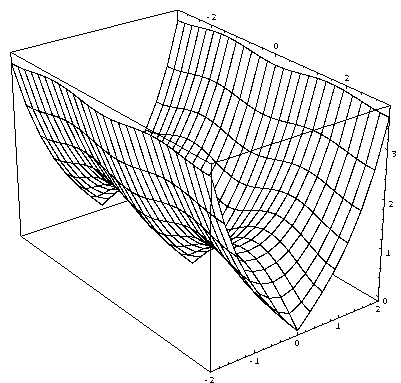
Funzione esponenziale
Input :=
Plot3D[Abs[Exp[z]], {x,-2, 1}, {y,-1.2, 1.2},
Shading -> False, BoxRatios -> {1,1,1},
ViewPoint -> {-2.3,-5.5, 2.}];

Commento: il grafico ottenuto mostra una superficie rigata (il valore assoluto dell'esponenziale dipende solo dalla parte reale di z).
 Funzione z -> 1/(z^2 + z + 1)
Funzione z -> 1/(z^2 + z + 1)
Input :=
Plot3D[Abs[1/(z^2+z+1)], {x,-1, 1}, {y,-1,1},
Shading->False, PlotPoints-> 30,
PlotRange -> {0,5}, BoxRatios -> {1,1,1}];
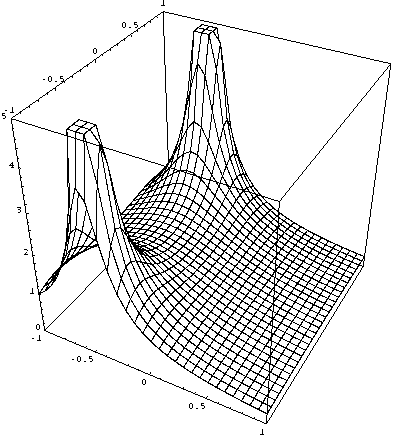
I due poli della funzione diventano punti in cui il valore assoluto della funzione stessa tende all'infinito.
Segnaliamo il volume di P. Antognini e G.C. Barozzi
Un breve introduzione al Sistema di Calcolo Mathematica di S. Wolfram.
Sommario: