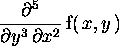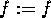
I comandi di derivazione con l'operatore D; il comando D(f)
ove f è una funzione di una variabile, calcola la derivata di f in senso funzionale:
> f:=x->f(x);
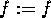
> D(f);
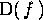
> D(tan);
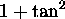
Regola di derivazione delle funzioni composte.
> f:=x->f(x);
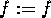
> g:=x->g(x);
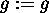
> D(f@g);
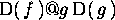
Il comando D[i](f)
ove f è una funzione di n variabili D[i](f) calcola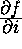 
, D[i,j](f) calcola 
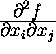; una derivata terza può essere ad esempio calcolata con il comando D[i](D[i,j](f)).
> f:=(x,y)->f(x,y);
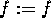
> D[1](f);
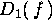
> D[2,1](f);
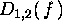
> f:=(x,y)->x^3*cos(x+y)^2;
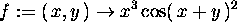
> D[2](D[1](f));
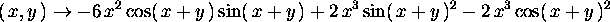
Un secondo comando di differenziazione: diff(a,x1,x2,..,xn),
ove a è una espressione nelle variabili successivamente indicate e x1,..,xn sono nomi di variabili; diff(f(x),x,x,x)=diff(f(x),x$3) calcola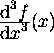 
e diff(g(x,y),x$2,y$3) calcola 
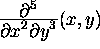; D(f)(x)=diff(f(x),x);
> diff(f(x),x);
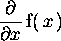
> diff(cos(x),x);
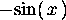
> diff(f(x,y),x);
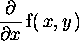
> diff(f(x,y),x$2,y$3);
