XCMODEL:
an aCADemic system
Giulio Casciola and Serena Morigi
Department of Mathematics
University of Bologna
Conference "ANALISI NUMERICA:
METODI E SOFTWARE MATEMATICO"
Ferrara 20/01/2000
What is XCMODEL?
a research and teaching laboratory to experiment and learn in a
graphics-interactive way;
an ideal environment to develop, perfect and compare methods and algorithms
in geometric modelling and graphic visualization.

What is
GEOMETRIC MODELLING?
A collection of methods for describing mathematically the object shape.
APPLICATIONS:
CAD/CAM/CAE; Computer Graphics; Robotics; Computer Vision;
Entertainment; FEM; Artificial Intelligence; GIS; Animation/
Simulation, ...
FIELDS:
Computational geometry; Analytical geometry; Topology; Linear algebra
; Approximation theory; Numerical Analysis; Computer Science.
XCMODEL
is based on NURBS
-
NURBS (Non Uniform Rational B-Spline)
De facto standards for the representation, design, and data exchange
of geometric data among different systems.
- Trimmed NURBS
Paradigm that allows for arbitrary domains overcoming the limit
of tensor product surfaces defined over rectangular regions.
- STANDARD AND GRAPHIC SYSTEMS INCLUDING NURBS
IGES (INITIAL GRAPHICS EXCHANGE SPECIFICATION)
STEP (STANDARD for the EXCHANGE of PRODUCT MODEL
DATA)
PHIGS++ (PROGRAMMER'S HIERARCHICAL INTERACTIVE
GRAPHICS SYSTEM)
IRIS-GL (SILICON GRAPHICS Inc.)
OPEN-GL (SILICON GRAPHICS Inc.)
STARBASE (HEWLETT-PACKARD Corp.)
RENDERMAN (PIXAR)
History
-
1989:
- Interests and activities on the geometric modelling field begins.
- 1991:
- A preliminary version of XCCURV initially only for spline curves , then for NURBS is realized.
- 1993:
- A preliminary version of XCSURF for NURBS is realized and
then evolved for TRIMMED NURBS.
- 1996:
- A robust, and efficient algorithm for the intersection of NURBS surfaces is devised; based on this, a first version of XCBOOL is then realized.
- 1996:
- An optimal ray tracing algorithm for NURBS is devised; based on this, a first version of XCRAYT is then realized.
- 1998:
- XCMODEL project beginning: we intend to realize an integrated
system incorporating the other packages for modelling and rendering.
- 20/01/2000:
- Release of the XCMODEL system, Version 1.0.
Scopes
-
User
- Reasearch and education
- Autonomy of the packages
- System evolution
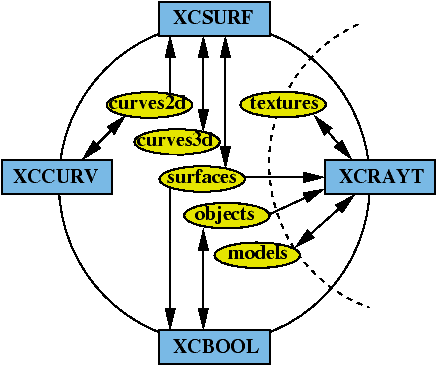
The packages of XCMODEL
- [xccurv] 2D modeller
- [xcsurf] 3D modeller
- [xcbool] solid modeller
[xcssi] surface intersection
[xcdbe] conversion tool for trimmed surfaces
[xctrim] visualization tool for trimmed surfaces
- [xcrayt] scene descriptor and renderer
[xhrayt,hrayt] ray-tracer
[xframe,xmovie] visualization tool for
images/animations
Technical Requirements
-
o UNIX O.S. and XWindow graphic system
- o Programming language ANSI-C
- o Utility Libraries required : Xlib, Xpm
- o Utility Libraries developped
-
MATRIX
- vectors and matrices computation
- descriptor
- scene descriptor
- trim
- visualization of trimmed NURBS surfaces in real time
- xtools
- GUI developper
- o Documentation for users: messages, help on-line, manuals,
on-line manuals
- o Documentation for developpers
- o Definition of the data formats: about 20 data format like standard supported
- o Release and Distribution
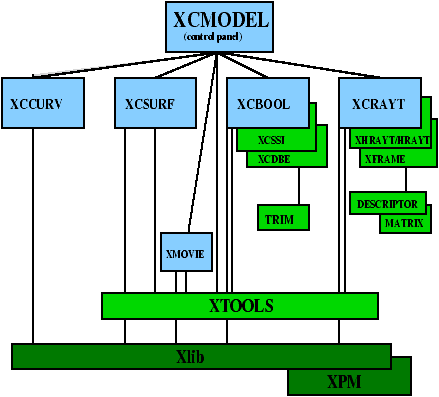
System Architecture
-
Number of source files ╗ 500
- Number of lines of code ╗ 120000
- Dimension for source code ╗ 3Mb
- Disk space used ╗ 10Mb (PC/Intel)
Documentation and Distribution
-
Web Page:
http://www.dm.unibo.it/~casciola/html/xcmodel.html
- Download binary versions (usr) for the following host architecture:
Sun, SGI e PC/Intel
- Download versions for developpers (dev) (work in progress)
- Download manuals (Version 1.0)
-
XCMODEL: a system to model and render NURBS curves and
surfaces, User's Guide
- XCCCURV: the 2D modeller, User's Guide
- XCSURF: the 3D modeller, User's Guide
- XCBOOL: the object composer, User's Guide
- XCRAYT: the scene descriptor, User's Guide
- MATRIX, Reference Manual
- DESCRIPTOR, Reference Manual
- TRIM, Reference Manual
- XTOOLS, Reference Manual
- Download data, models, images
Education
Courses:
-
o Metodi di Approssimazione,
Scienze dell' Informazione, UniversitÓ di Bologna 1993-1996;
- o Metodi Numerici per la Grafica, Informatica, UniversitÓ di Bologna, dal 1997;
- o Perfezionamento in "Matematica per le Applicazioni", Dip. Matematica, UniversitÓ Bologna, dal 1998;
- o SAMI, (Scuola per le Applicazioni della Matematica nell'Industria), corso INDAM, Milano, dal 1999;
Master Thesis:
-
o Mathematics;
- o Computer Science.
Credits
Research
SOLID MODELLING WITH NURBS:
G.Casciola, B.Quaquarelli,
Primitive solide, Operazioni Booleane e NURBS, Atti del
convegno internazionale ICO GRAPHICS '90, Milano febbraio 1990,
Mondadori.
SHAPE PRESERVING INTERPOLATION:
G.Casciola, Funzioni spline razionali di base,
XIV Congresso UMI, Catania (1991).
VISUALIZATION:
G.Casciola, R.Rossi,
Realizzazione di un algoritmo parallelo di ray tracing per
ipercubo Intel iPSC/2: strategie adottate e valutazione, Atti
del convegno internazionale ICO GRAPHICS '91, Milano marzo 1991,
Mondadori.
G.Casciola,
S.Morigi, Graphics in parallel computation for rendering 3D
modelled scenes, Parallel Computing 21 (1995).
NURBS SURFACES INTERSECTION:
G.Casciola, S.De
Santis, R.Quadalti, Algoritmi paralleli per il problema NURBS
Surface/Surface Intersection, Dipartimento di Matematica
Universitß di Bologna, dicembre 1992.
G.Casciola, S.Morigi, Il problema SSI
nella modellazione solida con superfici NURBS, Atti
dell'Accademia delle Scienze dell'Istituto di Bologna, (Febbraio
95)
REPARAMETRIZATION OF NURBS CURVES:
G.Casciola, S.Morigi, Riparametrizzazione di curve NURBS, XV
Congresso UMI, Padova (1995).
G.Casciola, S.Morigi, Reparametrization of NURBS curves, International Journal Shape Modelling Vol. 2, No.2&3 (1996)
DYNAMIC NURBS:
G.Casciola, G.L.Rubini, Sulle Dynamic
NURBS e la simulazione di processi dinamici, Rapporto Tecnico
CNR-IAC, Roma 1998.
P-SPLINE CURVES AND SURFACES:
S.Morigi,
Modellazione con curve e superfici P-spline (phD Thesis),
Quaderni GNIM-CNR (1997)
G.Casciola, M.Lacchini, S.Morigi, Degree elevation for
single-valued curves in polar coordinates, Department of
Mathematics, n.13, Bologna, Italy (1996)
G.Casciola, S.Morigi, Modelling of curves and surfaces in polar
and Cartesian coordinates, Department of Mathematics, n.12,
Bologna, Italy (1996)
G.Casciola, S.Morigi, Circle as p-spline curve,
Department of Mathematics, n.9, Bologna, Italy (1997).
G. Casciola, S. Morigi, Spline in polar and in
Cartesian coordinates, Curves and Surfaces with applications
in CAGD, A. LeMÚahutÚ, C. Rabut ed L.L. Schumaker (Eds.)
(1997)
G.Casciola, S.Morigi, J.SÓnchez-Reyes,
Degree elevation for p-BÚzier curves,
Computer Aided Geometric Design, Vol.15 (1998).
This document was translated from LATEX by HEVEA.