Scattered Data Fitting
The problem of approximating or interpolating scattered data
values f_k at the points P_k=(x_k,y_k), k=1,..,N inequally distributed in the
plane has been dealt with by many authors in the years.
Our contribution in this area were both in approximating than in
interpolating; more precisely in the first case we proposed a
polyalgorithm based on a Mean Weighted Method and on L-spline functions.
In this latter case we used tensor product natural L-splines defining a
grid domain containing the data and applying a least square fitting.
In the interpolating approach all the methods consists of three
different steps:
- triangulation of the data domain using the point P_k , k=1,..,N as the
vertices of the triangulation;
- a curve network is constructed interpolating the values F_k and approximating
the first-order partial derivatives on the subset consisting of the union of all
edges of the triangulation;
- an interpolation scheme is used in order to construct the global interpolation.
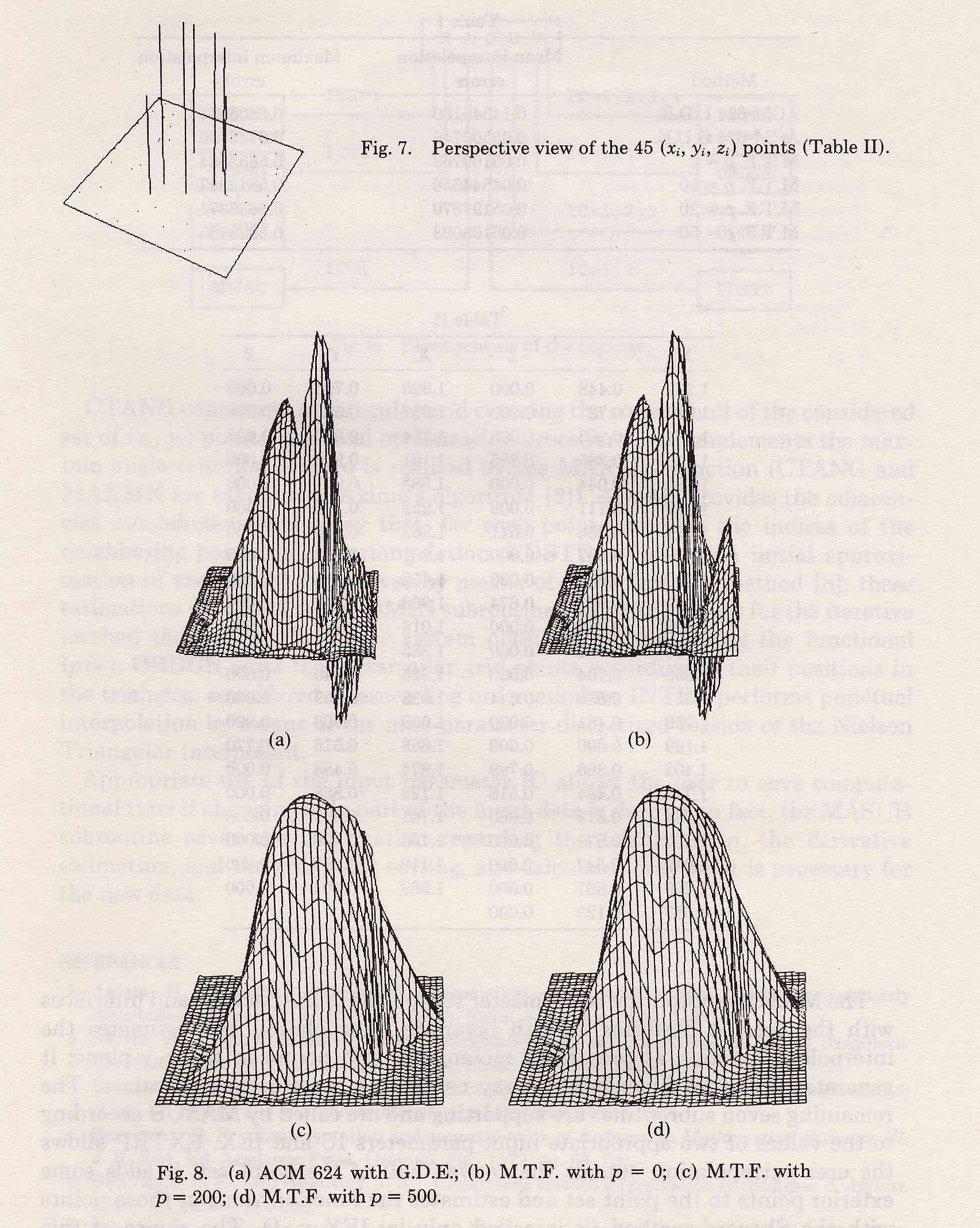
At the moment of our research in this topics all the known methods worked quite
well on relatively smooth data sets, but they failed for rapidly varying data.
In this case the reconstructed surface exhibited unwanted oscillations near
step gradients. Our proposal, published as ACM Algorithm 677, resolved this
problem giving to the user the means for controlling the behaviour of the
interpolating surface.
fitting data example
References
-
L.Bacchelli Montefusco, G.Casciola, Un polialgoritmo per la ricostruzione
di superfici mediante funzioni di forma locali,
Monografie di software matematico, n.1, IAC-Roma (1981).
-
L.Bacchelli Montefusco, G.Casciola, Interpolazione di funzioni bidimensionali
di classe C^1,
Monografie di software matematico, n.35, IAC-Roma (1984).
-
L.Bacchelli Montefusco, G.Casciola, C^1 surface interpolation, Algorithm
677,
ACM Transaction on Mathematical Software, vol.15, n.4 (1989).