Scientific Visualization


Our first work in computer graphics was a graphics library to visualize scalar functions in one and two variable and algebraic curves for a line printer. It was the 1979 and I were a young student interested to the visualization of our numerical results of interpolation and approximation problems.

Succesively my first work in 3D computer visualization was on a Tektronix 4105 storage tube in 1981. This page documents some of our research works about scientific visualization that can be resumed in rendering scalar functions of two variables in Cartesian and spherical coordinates by hidden-line algorithms.

The solution to many problem lies in scalar functions of two variables, the function being deriving either by an explicit description or a grid values. In such cases may be useful give a visual representation sufficiently realistic, but at the same time speedly.

The analyzed algorithms and our proposals were specific for the class of functions we dealt with. The research done was perfectly valid for its time. Moreover we well known that as conditions change, so do the algorithms.

Today, hardware acceleration, changes the relative costs of algorithms and so changes our ways of doing things. As example, we remember that some years ago, an algorithm described as ridiculously expensive, now is called Z-buffer and this hidden surface technique won out because it was easy to implement in hadware and because memory densities went up and cost went down.

Cartesian Coordinate examples

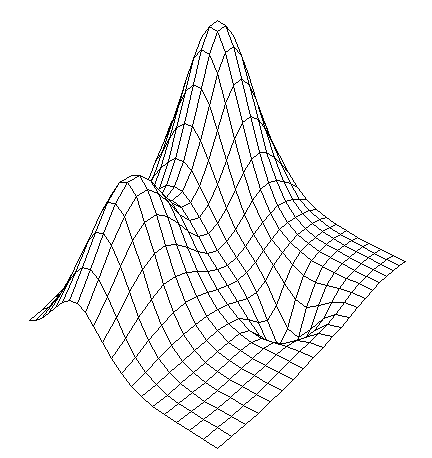Analitic function (grid 20x20) 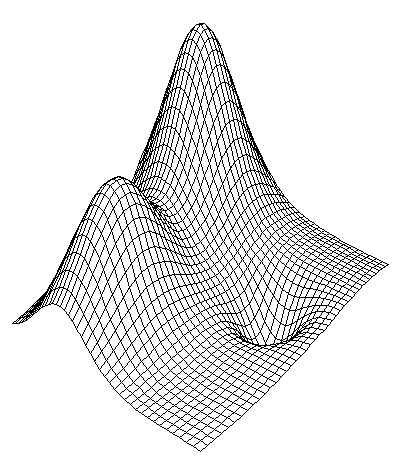Analitic function (grid 40x40)
Kubert function (grid 40x40) Kubert function (grid 60x60)

Spherical Coordinate examples

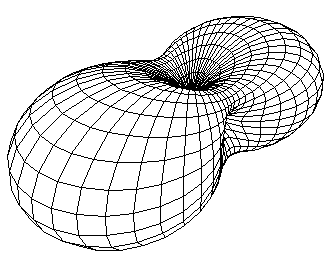dipolo function 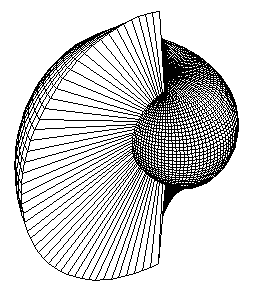shell function
lobo function star function

Recently, our Cartesian Coordinate Hidden Line Algorithm, has been implemented in Java Language and simply require the Java Virtual Machine.

References