Processing of 2D and 3D Image Sequences

Scaled-space and image enhancement techniques based on parabolic Partial Diffe rential Equations (PDEs) have proved to be powerful methods in the processing of two-dimensional (2D) and three-dimensional (3D) images and image sequences. Th ese models allow to include a-priori knowledge into the scale-space evolution, and they lead to an image simplification which simultaneously preserve or even enhance semantically important information such as edges, lines, or flow-like structures. Refer to the Sarti-Mikula-Sgallari paper for the ideas behind the different approaches for image or image sequence analysis as well as for the introduction of a new PDE model. Purpose of this r esearch is to analyze numerical schemes for these models for solving PDEs , base d on semi-implicit approximation in scale, finite-elements and finite volume in space and to consider the numerical linear algebra aspects involved in the meth ods and the related linear systems. Interesting applications of the PDE models for 2D and 3D image analysis have bee n investigating such as automatic image sequence restoration and image interpola tion of medical images.

Related publications:

* A.Sarti, K.Mikula, F.Sgallari, Nonlinear multiscale analysis of 3D echocardiographic sequences, in IEEE Transactions on Medical Imaging Vol.18, pp. 453-466, (1999)
* Morigi, S. Sarti, A. and Sgallari, F.,Parallel multiscale analysis of 2D image sequences, , in Proc. Fifth European SGI/CRAY MPP Workshop, Bologna, Italy, September 99 , (1999)
* Handlovicova, A., Mikula, K. and Sgallari, F.,Numerical methods for nonlinear diffusion equations arising in image processing, submitted(1999)

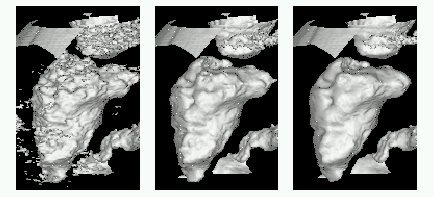
Picture3

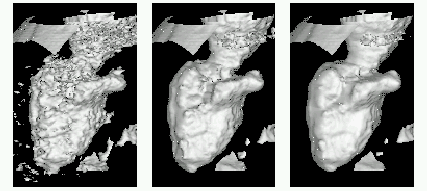
Picture4

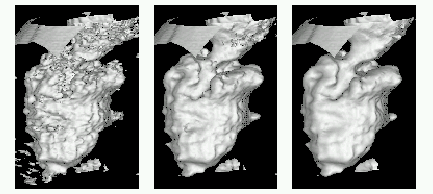
Picture5

Figures a-c. The multiscale analysis of 1st, 5th and 9th time step of the echocardiographic sequence. The shape of the left ventricle is extracted in those moments of cardiac cycle.

Return Return to Serena Morigi's Home Page