Alcune esperienze con MATLAB nella ricerca e didattica in Fisica Matematica
Tommaso Ruggeri
Relazione tenuta al Convegno Matlab organizzato dalla
Teoresi su: Il Mondo Numerico Incontra il Mondo
Reale - Bologna 14 Ottobre 1994.

Introduzione
Da molti anni
presso il nostro Centro Interdipartimentale di Ricerca per le applicazioni
della Matematica (C.I.R.A.M.) ci interessiamo
della problematica legata ad una didattica della Matematica in
seno alla Facoltà di Ingegneria che tenga conto dell enormi
possibilità che può offire l'uso del Computer.
In questo ambito abbiamo realizzato diversi libri e fascicoli sia
nel
settore dell'Analisi Matematica che in quello della
Meccanica Razionale [1]-[5].
In questi libri vengono associati ad esercizi di tipo
tradizionale anche problematiche che richiedono un'indagine numerica.
In questi ultimi allo studente non viene richiesto di realizzare
di fatto un programma, ma soltanto che egli sappia concepire
un ordine logico (del tipo flow-chart) necessario
alla realizzazione di un ipotetico programma. Un esercizio in tal
senso richiede da parte dello studente, oltre
che una precisa conoscenza degli
argomenti sviluppati nella teoria, anche un accurato esame dei particolari
nonchè una seppur minima conoscenza di argomenti di analisi numerica.
Per ciascuna di queste esercitazioni viene fornita dagli autori
una possibile soluzione e proposto un programma che si trova
accluso nel software a corredo.
Tali programmi possono poi essere utilizzati per la risoluzione dei
rimanenti esercizi proposti.
L'utilizzazione del P.C. viene quindi vista come strumento didattico
non passivo, ma atto a stimolare l'apprendimento di tecniche numeriche
e grafiche che il calcolatore ha il pregio di svolgere in tempi brevi.
In altre circostanze gli aspetti numerici sono un effettivo
completamento all'analisi qualitativa laddove non è possibile
ricavare con carta e penna la soluzione esplicita dei problemi
(si pensi, per esempio, alle
equazioni differenziali non-lineari).
Naturalmente questi supporti diventano utili solo quando tutta la
didattica (lezioni ed esercitazioni) sia in sintonia con una
tale filosofia. Nell'esperienza sopra menzionata, gli autori
durante le ore di esercitazioni si avvalevano di P.C. portatili
dotati di un'interfaccia per lavagna luminosa e integravano
esercitazioni e lezioni utilizzando di volta in volta i relativi
programmi.
Questo ovviamente comporta preliminarmente
la realizzazione di strutture
idonee e di docenti disponibili a modificare, seppure di poco,
la didattica tradizionale. è opinione di molti che questa sia
una buona strada anche per la riconosciuta accoglienza favorevole
che gli studenti hanno manifestato laddove questi esperimenti
hanno avuto luogo.
Da qualche tempo a questa parte, abbiamo provato ad utilizzare a questi fini il programma MATLAB che grazie alla sua potenza di calcolo e, nell'ultima release, le sue
enormi capacità grafiche, permette con pochi passi di programma di raggiungere velocemente il risultato, senza doversi preoccupare di fatti numerici marginali alle questioni trattate.
In questa breve relazione, desidero, limitandomi al settore della Fisica Matematica, fornire alcuni esempi di come sia possibile realizzare alcuni brevi ma efficaci programmi che
aiutano lo studente a meglio comprendere la disciplina che sta studiando.
Infine presenterò anche un esempio di utilizzo di MATLAB in un argomento di ricerca che stiamo portando avanti con il gruppo di Fisica Matematica del CIRAM.

Esempio n.1: Il Computer permette di
comprendere meglio un problema.
Il primo esempio, consiste di far comprendere bene ed in maniera interattiva, come
le componenti di un operatore matriciale cambiano al cambiare della base.
Considerando il caso di matrici 2 x 2 simmetriche, si modifica mediante
il comando di ginput la direzione degli assi e si riscrive la matrice mediante
la trasformazione di similitudine. Man mano che ci si avvicina alla direzione degli autovettori, lo studente osserva che gli elementi della diagonale
principale tendono agli autovalori mentre le restanti componenti tendono a zero.
Basta un esempio come questo per attirare l'attenzione degli studenti in maniera più efficace che qualsiasi altra esercitazione di tipo tradizionale sull'argomento.
Le prime due figure mostrano le comonenti dell'operatore rispetto alla
base di partenza e rispetto alla base degli autovettori.
Ecco il listato che realizza il programa in matlab:
figure('Position',[10 400 600 300])
xpsubplt(1,2,1);
f=[1 5
5 9];
pltmat(f,'F','m',15);
xpsubplt(1,2,2);
plot([-1 1],[0 0],'y',[0 0],[-1 1],
'r',1,0,'yo',0,1,'ro');
axis([-1.5 1.5 -1.5 1.5]);
title('Cambiamento Base ed Autovettori');
but=1;
while but==1
[x,y,but]=ginput(1);
dist=sqrt(x^2+y^2);
r=[y/dist -x/dist
x/dist y/dist];
f1=r'*f*r;
xpsubplt(1,2,1);
pltmat(f1,'F','m',15);
xpsubplt(1,2,2);
plot([-y/dist y/dist],[x/dist -x/dist],'y',
[-x/dist x/dist],[-y/dist y/dist],'r',
y/dist,-x/dist,'yo',x/dist,y/dist,'ro',
[-1 1],[0 0],'y',[0 0],[-1 1],
'r',1,0,'yo',0,1,'ro');
axis([-1.5 1.5 -1.5 1.5]);
title('Cambiamento Base ed Autovettori');
end
xpsubplt(1,2,2);
[d1,l1]=eig(f);
dist=1;
r=[d1(1,2) d1(1,1)
d1(2,2) d1(2,1)];
f1=r'*f*r;
xpsubplt(1,2,1);
pltmat(f1,'F','m',10);
xpsubplt(1,2,2);
x=r(2,1);
y=r(1,1);
plot([-y/dist y/dist],[x/dist -x/dist],
'y',[-x/dist x/dist],[-y/dist y/dist],
'r',y/dist,-x/dist,'yo',
x/dist,y/dist,'ro',[-1 1],[0 0],'y',
[0 0],[-1 1],'r',1,0,'yo',0,1,'ro');
axis([-1.5 1.5 -1.5 1.5]);
title('Cambiamento base ed Autovettori');
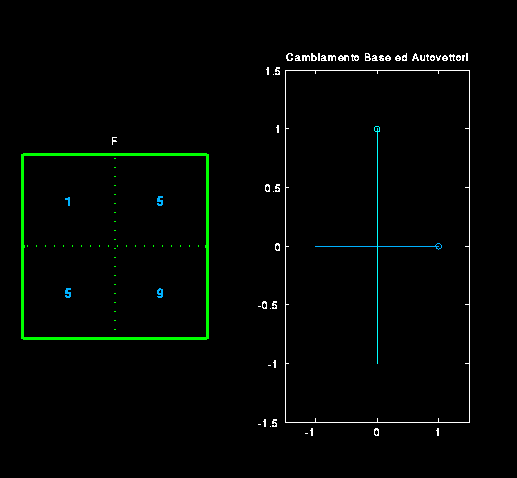
Matrice iniziale.
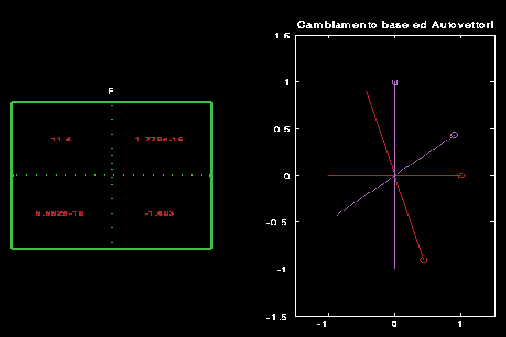
Matrice rispetto alla base degli autovettori.

Esempio n.2: Il Computer pone ulteriori problemi!
Un classico problema di Meccanica è quello
dell'equilibrio di un corpo rigido pesante appoggiato in un numero finito n di punti
su un
piano orizzontale liscio. Come è ben noto l'equilibrio sussiste purchè
il
centro di pressione sia non esterno al poligono di appoggio.
Tale poligono
possiede i seguenti tre requisiti:
- i vertici del poligono sono punti di appoggio;
- i punti di appoggio che non sono vertici non sono esterni al poligono;
- il poligono è convesso.
Supponendo di conoscere le coordinate cartesiane dei punti di appoggio
è estremamente semplice per un qualsiasi studente disegnare,
in base alle caratteristiche sopra menzionate il poligono.
Rimane quindi come unico restante
problema il calcolo delle reazioni vincolari nei punti di appoggio.
Dal punto di vista di un programmatore si pone però
un problema aggiuntivo rispetto a quello tradizionale, non essendo
il computer dotato di occhi per vedere i punti!
Bisogna infatti ideare
un procedimento numerico atto a costruire il
poligono avendo a disposizione soltanto i valori numerici delle
coordinate dei punti di appoggio.
Agli studenti in aula viene quindi presentata una nuova problematica.
È interessante osservare
come ogni anno vi è sempre l'intervento di studenti che indicano
alcune possibili soluzioni del problema.
Una di queste è la seguente:
fissiamo inizialmente
due punti di appoggio distinti 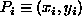 e
e 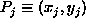 con
con 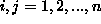 .
Per stabilire se la congiungente tali punti è un lato del poligono
si valuta la distanza, con segno, tra la retta
.
Per stabilire se la congiungente tali punti è un lato del poligono
si valuta la distanza, con segno, tra la retta 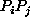 e ciascuno dei restanti punti di appoggio
e ciascuno dei restanti punti di appoggio 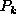 :
:
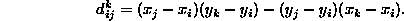
Se per ogni 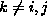 tutte le distanze
tutte le distanze 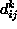 hanno lo stesso segno, sicuramente il
lato
hanno lo stesso segno, sicuramente il
lato 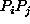 appartiene al poligono di appoggio e viene fatto disegnare.
Allo studente non rimane che concepire
una breve parte di calcolo per poter
valutare anche le reazioni vincolari supponendo la piccola
cedevolezza lineare del suolo e determinare gli eventuali punti di
distacco.
La fig. 3 rappresenta un esempio della schermata grafica
fornita dal programma realizzato con Matlab.
Valori negativi delle reazioni (come in figura) si interpretano come distacco dei corrispondenti punti di appoggio. In tal caso è necessario ricostruire
il poligono di appoggio scartando questi punti e ripetendo
il calcolo delle reazioni.
appartiene al poligono di appoggio e viene fatto disegnare.
Allo studente non rimane che concepire
una breve parte di calcolo per poter
valutare anche le reazioni vincolari supponendo la piccola
cedevolezza lineare del suolo e determinare gli eventuali punti di
distacco.
La fig. 3 rappresenta un esempio della schermata grafica
fornita dal programma realizzato con Matlab.
Valori negativi delle reazioni (come in figura) si interpretano come distacco dei corrispondenti punti di appoggio. In tal caso è necessario ricostruire
il poligono di appoggio scartando questi punti e ripetendo
il calcolo delle reazioni.
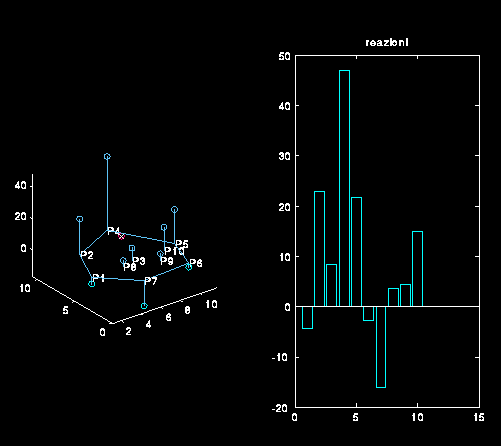
Poligono di appoggio e reazioni vincolari.

Esempio n.3: Il Computer non permette superficialità.
Come è noto vi sono teoremi la cui dimostrazione è costruttiva. Pertanto
l'ideazione di un programma o perlomeno di un flow-chart permette allo
studente di chiarire nei minimi dettagli la stessa dimostrazione. Un tipico
esempio è costituito dal Teorema Polare dell'algebra lineare che ha
molteplici applicazioni nella Meccanica dei Continui deformabili. Il quesito
proposto agli studenti nel nostro Laboratorio è il seguente:
Descrivere le fasi logiche necessarie per la realizzazione di un programma
che permetta, dato un operatore matriciale 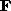 con
con 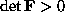 , di determinare la
matrice di rotazione
, di determinare la
matrice di rotazione 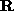 e le dilatazioni
e le dilatazioni 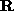 e
e 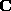 tali che
tali che
 Per semplicità, nella realizzazione pratica del programma, si consideri il
caso in cui F è
Per semplicità, nella realizzazione pratica del programma, si consideri il
caso in cui F è 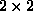 .
.
Le varie fasi necessarie per la costruzione di 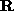 ,
, 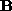 e
e 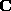 sono le seguenti.
Bisogna dapprima calcolare la matrice
sono le seguenti.
Bisogna dapprima calcolare la matrice 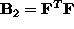 che è sicuramente simmetrica
e definita positiva. Nel caso
che è sicuramente simmetrica
e definita positiva. Nel caso 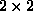 è facile anche calcolare gli autovalori
gli autovalori
è facile anche calcolare gli autovalori
gli autovalori 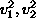 (tutti positivi) di
(tutti positivi) di 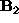 e i corrispondenti autovettori (ortogonali e
scelti normalizzati)
e i corrispondenti autovettori (ortogonali e
scelti normalizzati)
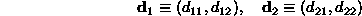
Si costruisce quindi il relativo operatore di rotazione

Rispetto alla base 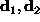 , la matrice
, la matrice 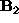 è diagonale e si può costruire
l'operatore
è diagonale e si può costruire
l'operatore

anch'esso simmetrico e definito positivo, nonchè 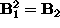 . Mediante la
trasformazione di similitudine indotta da
. Mediante la
trasformazione di similitudine indotta da 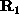 si ottiene l'operatore
si ottiene l'operatore 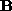 :
:

L'operatore di rotazione si ricava da

Infine la dilatazione 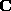 si ottiene per trasformazione di similitudine
(mediante
si ottiene per trasformazione di similitudine
(mediante 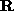 ) da
) da 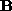 :
:

Il punto più delicato della dimostrazione stà nella necessità di passare
dalla base di partenza a quella degli autovettori e ritornare poi a quella
di prima per poter costruire la dilatazione 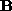 . Inoltre lo studente deve
avere un quadro preciso di buona parte degli argomenti tipici dell'algebra
lineare: operatore di rotazione, operatore inverso, trasformazioni di
similitudine, autovalori ed autovettori, ecc... Di seguito viene riportato
il listato ed alcune figure relative a questo problema.
. Inoltre lo studente deve
avere un quadro preciso di buona parte degli argomenti tipici dell'algebra
lineare: operatore di rotazione, operatore inverso, trasformazioni di
similitudine, autovalori ed autovettori, ecc... Di seguito viene riportato
il listato ed alcune figure relative a questo problema.
pltmat(['F=RB';'F=CR'],'Teorema Polare','m',18)
pause
%f=input('dammi F =');
f=[1 2
-1 3];
pltmat(f,'F','m',18);
pause
b2=f'*f;
b=sqrtm(b2);
pltmat(b,'B','m',18);
pause
r=f*b^(-1);
pltmat(r,'R','m',18);
pause
c=r*b*r';
pltmat(c,'C','m',18);
pause
xpsubplt(1,3,1);
pltmat(f,'F','g',10);
xpsubplt(1,3,2);
pltmat(r,'R','w',10);
xpsubplt(1,3,3)
pltmat(b,'B','r',10);
pause
xpsubplt(1,3,1);
pltmat(f,'F','g',10);
xpsubplt(1,3,2);
pltmat(c,'C','w',10);
xpsubplt(1,3,3)
pltmat(r,'R','r',10);
pause
xpsubplt(2,2,1);
pltmat(f,'F','m',12);
xpsubplt(2,2,2);
pltmat(r*b,'R B','g',12);
xpsubplt(2,2,3);
pltmat(r*r','R Rt','r',9);
xpsubplt(2,2,4);
pltmat(eig(b),'eig(B)','w',12);
pause
xpsubplt(2,2,1);
pltmat(f,'F','m',12);
xpsubplt(2,2,2);
pltmat(c*r,'C R','g',12);
xpsubplt(2,2,3);
pltmat(r*r','R Rt','r',9);
xpsubplt(2,2,4);
pltmat(eig(c),'eig(C)=eig(B)','w',12);
pause
xpsubplt(1,1,1);
axis([-1 4 -1 4]);
hold on
x0=[0,0,1,1,0];
y0=[1,0,0,1,1];
v1=[0; 1];
v3=[1; 0];
w1=b*v1;
w3=b*v3;
z1=r*w1;
z3=r*w3;
x1=[0, w3(1,1), w3(1,1)+w1(1,1), w1(1,1), 0];
y1=[0, w3(2,1), w3(2,1)+w1(2,1), w1(2,1), 0];
x2=[0, z3(1,1), z3(1,1)+z1(1,1), z1(1,1), 0];
y2=[0, z3(2,1), z3(2,1)+z1(2,1), z1(2,1), 0];
axis('square');
title('Teorema Polare F = C R');
patch(x0,y0,'r');
title('Corpo indeformato v');
pause
patch(x1,y1,'y');
patch(x0,y0,'r');
title('La dilatazione B v');
pause
patch(x2,y2,'b');
patch(x1,y1,'y');
patch(x0,y0,'r');
title('La rotazione finale R B v = F v');
pause
w1=r*v1;
w3=r*v3;
z1=c*w1;
z3=c*w3;
x1=[0, w3(1,1), w3(1,1)+w1(1,1), w1(1,1), 0];
y1=[0, w3(2,1), w3(2,1)+w1(2,1), w1(2,1), 0];
x2=[0, z3(1,1), z3(1,1)+z1(1,1), z1(1,1), 0];
y2=[0, z3(2,1), z3(2,1)+z1(2,1), z1(2,1), 0];
title('Teorema Polare F = C R');
patch(x0,y0,'r');
title('Corpo indeformato v');
pause
patch(x1,y1,'g');
patch(x0,y0,'r');
title('La rotazione R v');
pause
patch(x2,y2,'b');
patch(x1,y1,'g');
patch(x0,y0,'r');
title('La dilatazione finale C R v = F v');
hold off
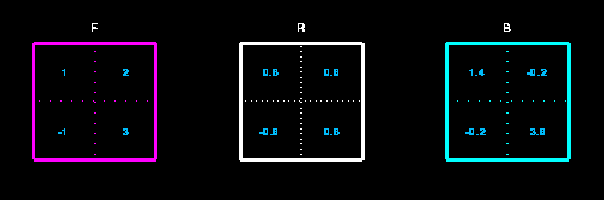

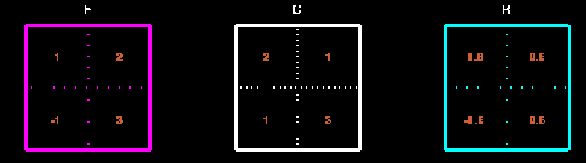

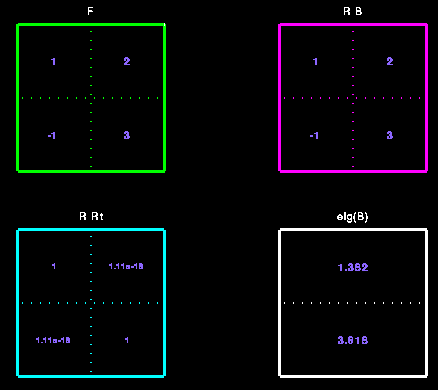
Controllo: 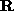 = rotazione,
= rotazione, 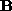 definita positiva.
definita positiva.
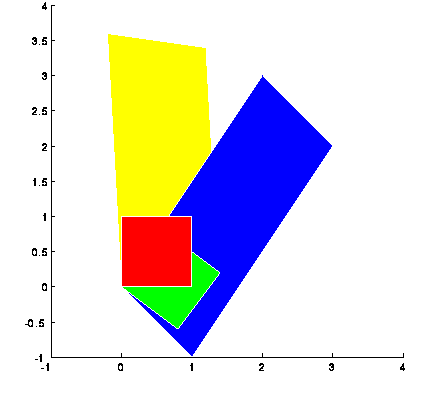
Applicazione grafica del teorema polare in un problema di deformazione
omogenea. Si parte dal quadrato rosso e si applica la dilatazione 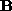 ottenendo il disegno in giallo e quindi si applica l'operatore di rotazione
ottenendo il disegno in giallo e quindi si applica l'operatore di rotazione
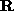 . Oppure si fa prima la rotazione e poi la dilatazione passando dal
rosso-verde-blu.
. Oppure si fa prima la rotazione e poi la dilatazione passando dal
rosso-verde-blu.

Esempio n.4: Analisi qualitativa e Grafica
Come abbiamo detto nell'introduzione
l'usare Matlab permette di determinare
soluzioni numeriche di sistemi dinamici non lineari.
Le possibilità grafiche offrono allo studente una maniera espressiva
ed immediata per comprendere l'aspetto fisico e l'analisi qualitativa.
Nella figura 6 è riportata l'immagine prodotta
dal programma diff2.m che fornisce la soluzione di un'equazione differenziale non lineare del secondo ordine e la traiettoria nel piano di fase.
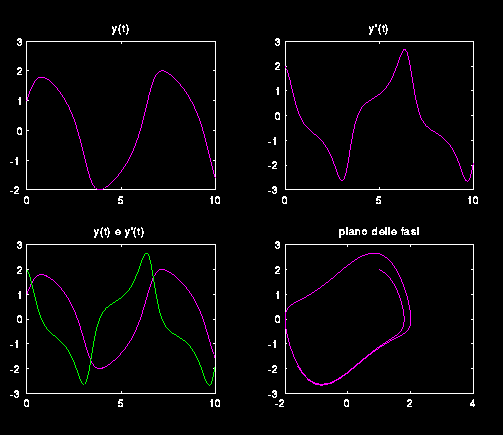
Sono attive quattro finestre grafiche che forniscono rispettivamente
la funzione, la derivata, il piano delle fasi.
Vi è anche è la possibilità di prolungare il tempo
in modo da visualizzare un comportamento asintotico.
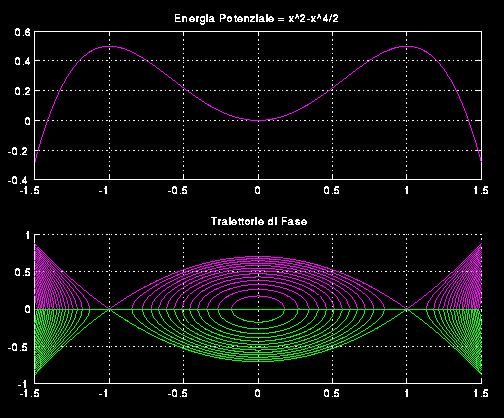
Infine, in figura 7 viene
rappresentato un esempio di energia potenziale
e il corrispondente diagramma di fase ottenuto con il
programma pfase.m

Equazione alle derivate parziali: Interazioni tra Onde lineari
Vogliamo, adesso mostrare come con pochissime righe scritte in Matlab sia
possibile visualizzare l'evoluzione e l'interazione di onde lineari
soluzioni della classica equazione iperbolica del secondo ordine alle derivate parziali per la funzione incognita
u(x,t):
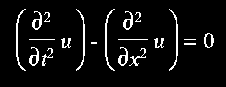
Prendiamo un dato iniziale che abbia derivata nulla e u(x,0) che vale zero eccetto in due intervalli in cui ha
la forma di un seno (vedi figura 8). Il dato iniziale viene scritto come
funzione .m nel file ondad.m
function y=ondad(x);
y=(x> -2).*(x< -1).*sin(-(x+1)*pi)+
2*(x>1).*(x<2).*sin((x-1)*pi);
end
Basta allora scrivere la soluzione fondamentale, per avere subito la visualizzazione dell'evoluzione ed interazione delle onde (figg. successive).
x=-5:.01:5;
plot(x,ondad(x));
%axis([-1 2 0 1]);
pause
for t=0:.04:2.4;
x1=x-t;
x2=x+t;
y=(ondad(x1)+ondad(x2))/2;
plot(x,y)
%axis([-1 2 0 1]);
drawnow
end
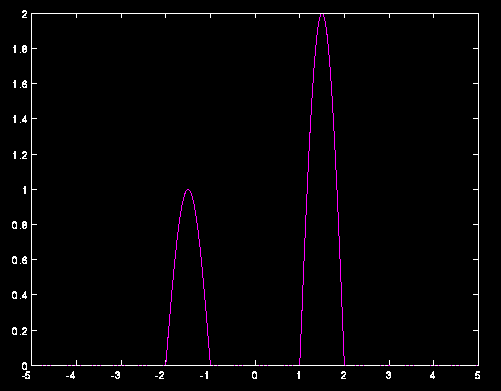
Fig.8: Onde iniziali
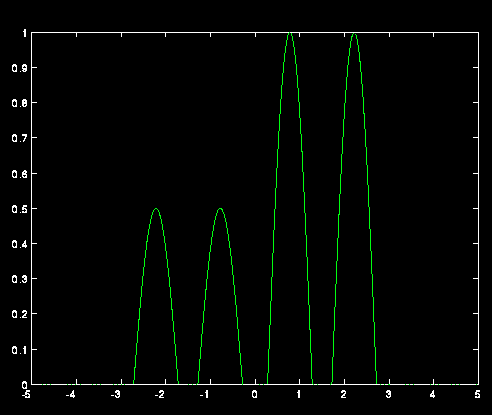
Le due onde evolvono in altre due onde.
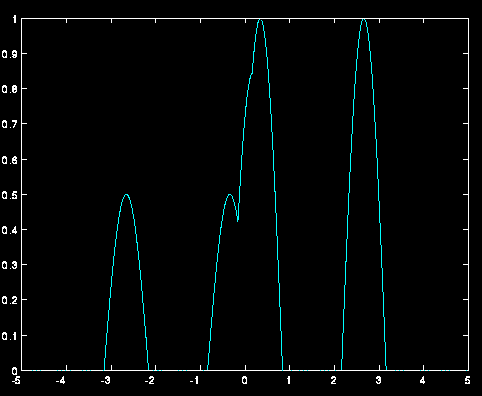
Interazioni tra due onde
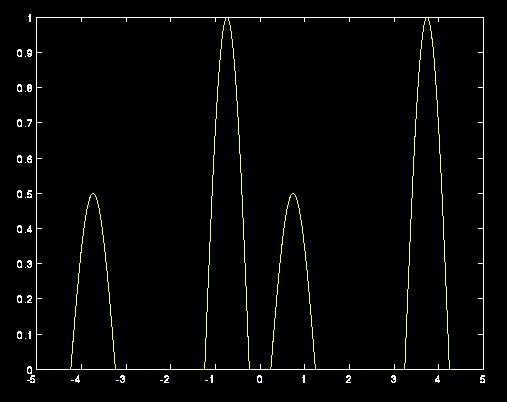
Le quattro onde finali.

Esempio n.6: Mappe ed Attrattore di Henon
Come ultimo esempio nella didattica, voglio portare un caso in cui il Computer
fa la parte effettivamente del protagonista. Questo è un prototipo della problematica non lineare che riguarda gli argomenti attuali del caos, frattali, attrattori strani, ecc...
Si consideri la Mappa quadratica:
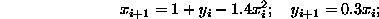
al variare dell'intero i=1,2..., si rappresenta il punto di coordinate 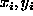 e si osserva che i punti si distribuiscono in maniera caotica, ma al
crescere del numero di iterazioni vanno ad infittirsi in una regione a forma
di cometa nel piano (attrattore strano) (vedi fig. 12)
e si osserva che i punti si distribuiscono in maniera caotica, ma al
crescere del numero di iterazioni vanno ad infittirsi in una regione a forma
di cometa nel piano (attrattore strano) (vedi fig. 12)
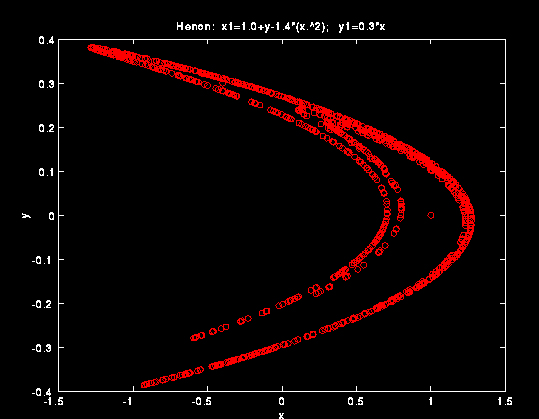
Attrattore di Henon.

Un Esempio nella Ricerca: Onde non lineari
Per finire desidero portare un esempio di utilizzo di Matlab in una ricerca che ho svolto
insieme al Prof. Muracchini ed al dott. Seccia [6]. Il problema riguarda la seguente problematica di Fisica delle basse temperature.
Sperimentalmente si è osservato che prendendo un campione di cristallo e portandolo
a temperature dell'ordine di pochi gradi Kelvin, una perturbazione di temperatura creata ad
un estremo del campione si propaga come un'onda in contrasto con l'usuale equazione parabolica del calore. Tale fenomeno conosciuto come secondo suono era stato in precedenza rilevato nell'elio superfluido. Diverse teorie del secondo suono esistono in letteratura, ma allo stato attuale non sono sufficienti a spiegare due aspetti del fenomeno che invece sono abbastanza evidenti negli esperimenti. Il primo è quello che la velocità di propagazione del secondo suono dipende fortemente dal valore della temperatura imperturbata To, ed il secondo che la forma dell'onda cambia durante l'evoluzione, al cambiare di To. In alcuni lavori
abbiamo proposto un modello altamente non lineare, che utilizzando la metodologia della
Termodinamica Estesa (ET), permette di spiegare questi due aspetti del fenomeno.
Utilizzando la potenza di Matlab abbiamo anche fatto una simulazione numerica della propagazione dell'onda di secondo suono.
Riportiamo di seguito la simulazione ottenuta per un cristallo di NaF.
Nella figura 13 vi è l'onda termica iniziale a forma di un gaussiana che innalza la temperatura da 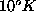 ad
ad 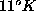 e nella figura 14 vi è l'evoluzione
dell'onda all'istante in cui la soluzione cessa di essere di classe
e nella figura 14 vi è l'evoluzione
dell'onda all'istante in cui la soluzione cessa di essere di classe 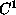 .
Mentre la figura 15 riporta l'evoluzione nel caso di temperatura
imperturbata del campione di
.
Mentre la figura 15 riporta l'evoluzione nel caso di temperatura
imperturbata del campione di 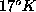 . Come si osserva facilmente passando da
. Come si osserva facilmente passando da
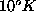 (fig. 14) a
(fig. 14) a 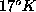 (fig.15) la forma dell'onda subisce un cambiamento
di forma opposto che sembra confermato negli esperimenti.
(fig.15) la forma dell'onda subisce un cambiamento
di forma opposto che sembra confermato negli esperimenti.
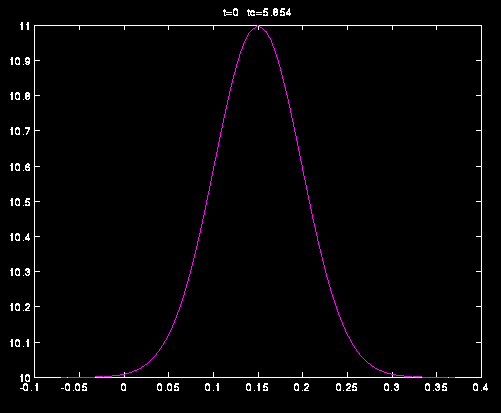
Onda iniziale.
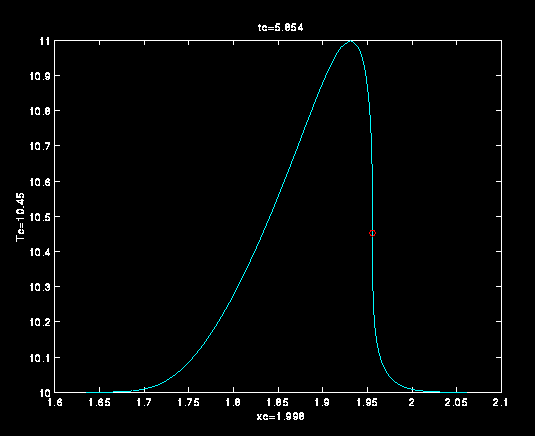
Evoluzione dell'onda per temperatura imperturbata di 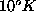 .
.
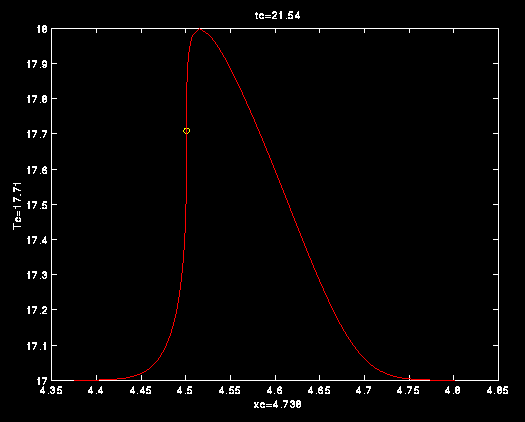
Evoluzione dell'onda per temperatura imperturbata di 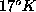 .
.

Bibliografia
- S. Matarasso e T. Ruggeri, Laboratorio di Matematica - Primo Corso: Temi di Analisi Matematica e
Software Matematico.
Progetto Leonardo - Esculapio Ed. Bologna (1991).
- A. Muracchini, T. Ruggeri e L. Seccia, Laboratorio di Meccanica Razionale: Esercizi, Temi di esame e
Software Matematico. Progetto Leonardo - Esculapio Ed. Bologna (1991).
- S. Matarasso e T. Ruggeri, Labmat2 - Dispense di Analisi Matematica II con l'utilizzo
di Software Matematico. Vol. 1: Funzioni reali di più
variabili; Applicazioni nel campo complesso; Programma Tredimw.exe.
Progetto Leonardo - Esculapio Ed. Bologna (1993).
- S. Matarasso e T. Ruggeri, Labmat2 - Dispense di Analisi Matematica II con l'utilizzo
di Software Matematico. Vol. 5: Elementi di Equazioni
differenziali con esempi di dinamica del punto;
Temi di esame di Analisi II; Programma Diff2w.exe;
Worksheets con Maple V.
Progetto Leonardo - Esculapio Ed. Bologna (1994).
- Didattica Matematica con l'ausilio del Personal Computer
a cura di R. Guidorzi e T. Ruggeri - Pubbl. del CCIB e CIRAM -
Pitagora (1992).
- T. Ruggeri, A. Muracchini e L. Seccia,
Shock Waves and Second Sound in a Rigid Heat conductor.
A critical temperature for NaF and Bi. Phys. Rev. Lett. 64, n.22, pp. 2640-2643 (1990).
A Continuum Approach to Phonon Gas and Shape Changes of Second
Sound via Shock Waves Theory, Nuovo Cimento D, 16,1, pp.15-44 (1994).
- I. Müller e T. Ruggeri,
Extended Thermodynamics,
Springer Tracts on Natural Philosophy 37 - Springer Verlag - New
York (1993).
Back to Ruggeri home page
Back to CIRAM home page






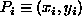 e
e 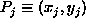 con
con 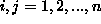 .
Per stabilire se la congiungente tali punti è un lato del poligono
si valuta la distanza, con segno, tra la retta
.
Per stabilire se la congiungente tali punti è un lato del poligono
si valuta la distanza, con segno, tra la retta 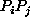 e ciascuno dei restanti punti di appoggio
e ciascuno dei restanti punti di appoggio 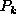 :
:
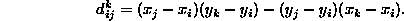
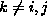 tutte le distanze
tutte le distanze 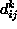 hanno lo stesso segno, sicuramente il
lato
hanno lo stesso segno, sicuramente il
lato 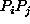 appartiene al poligono di appoggio e viene fatto disegnare.
Allo studente non rimane che concepire
una breve parte di calcolo per poter
valutare anche le reazioni vincolari supponendo la piccola
cedevolezza lineare del suolo e determinare gli eventuali punti di
distacco.
La fig. 3 rappresenta un esempio della schermata grafica
fornita dal programma realizzato con Matlab.
Valori negativi delle reazioni (come in figura) si interpretano come distacco dei corrispondenti punti di appoggio. In tal caso è necessario ricostruire
il poligono di appoggio scartando questi punti e ripetendo
il calcolo delle reazioni.
appartiene al poligono di appoggio e viene fatto disegnare.
Allo studente non rimane che concepire
una breve parte di calcolo per poter
valutare anche le reazioni vincolari supponendo la piccola
cedevolezza lineare del suolo e determinare gli eventuali punti di
distacco.
La fig. 3 rappresenta un esempio della schermata grafica
fornita dal programma realizzato con Matlab.
Valori negativi delle reazioni (come in figura) si interpretano come distacco dei corrispondenti punti di appoggio. In tal caso è necessario ricostruire
il poligono di appoggio scartando questi punti e ripetendo
il calcolo delle reazioni.


![]() con
con ![]() , di determinare la
matrice di rotazione
, di determinare la
matrice di rotazione ![]() e le dilatazioni
e le dilatazioni ![]() e
e ![]() tali che
tali che

![]() ,
, ![]() e
e ![]() sono le seguenti.
Bisogna dapprima calcolare la matrice
sono le seguenti.
Bisogna dapprima calcolare la matrice ![]() che è sicuramente simmetrica
e definita positiva. Nel caso
che è sicuramente simmetrica
e definita positiva. Nel caso ![]() è facile anche calcolare gli autovalori
gli autovalori
è facile anche calcolare gli autovalori
gli autovalori ![]() (tutti positivi) di
(tutti positivi) di ![]() e i corrispondenti autovettori (ortogonali e
scelti normalizzati)
e i corrispondenti autovettori (ortogonali e
scelti normalizzati)
![]()
![]()
![]() , la matrice
, la matrice ![]() è diagonale e si può costruire
l'operatore
è diagonale e si può costruire
l'operatore
![]()
![]() . Mediante la
trasformazione di similitudine indotta da
. Mediante la
trasformazione di similitudine indotta da ![]() si ottiene l'operatore
si ottiene l'operatore ![]() :
:
![]()
![]()
![]() si ottiene per trasformazione di similitudine
(mediante
si ottiene per trasformazione di similitudine
(mediante ![]() ) da
) da ![]() :
:
![]()
![]() . Inoltre lo studente deve
avere un quadro preciso di buona parte degli argomenti tipici dell'algebra
lineare: operatore di rotazione, operatore inverso, trasformazioni di
similitudine, autovalori ed autovettori, ecc... Di seguito viene riportato
il listato ed alcune figure relative a questo problema.
. Inoltre lo studente deve
avere un quadro preciso di buona parte degli argomenti tipici dell'algebra
lineare: operatore di rotazione, operatore inverso, trasformazioni di
similitudine, autovalori ed autovettori, ecc... Di seguito viene riportato
il listato ed alcune figure relative a questo problema.

![]()

![]()

![]() = rotazione,
= rotazione, ![]() definita positiva.
definita positiva.

![]() ottenendo il disegno in giallo e quindi si applica l'operatore di rotazione
ottenendo il disegno in giallo e quindi si applica l'operatore di rotazione
![]() . Oppure si fa prima la rotazione e poi la dilatazione passando dal
rosso-verde-blu.
. Oppure si fa prima la rotazione e poi la dilatazione passando dal
rosso-verde-blu.




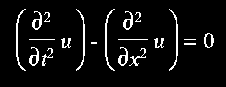





![]()
![]() e si osserva che i punti si distribuiscono in maniera caotica, ma al
crescere del numero di iterazioni vanno ad infittirsi in una regione a forma
di cometa nel piano (attrattore strano) (vedi fig. 12)
e si osserva che i punti si distribuiscono in maniera caotica, ma al
crescere del numero di iterazioni vanno ad infittirsi in una regione a forma
di cometa nel piano (attrattore strano) (vedi fig. 12)





