Processing of 2D and 3D Echo Image Sequences
Fiorella
Sgallari
CIRAM – Dept. of Mathematics,
University of Bologna, Italy
Karol Mikula: Department of Mathematics,
Slovak University of Technology, Slovakia
Alessandro Sarti:
DEIS, University of Bologna,Italy
TecnoBiomedica, Roma; http://www.tecnobiomedica.it
ESAOTE Spa, Genova; http://www.esaote.com/
In many applications computers analyse images or image sequences which are often contaminated by noise, and their quality can be poor (e.g. in medical imaging). We have studied mathematical models based on partial differential equations (PDEs) approach to automatically produce images of much higher quality, with enhanced sharpness, filtered out the noise, extracted shapes, closed missing boundaries, etc. We have designed and analysed the robust numerical methods and their efficient implementations in processing of 2D, 3D images, 2D+time and 3D+time image sequences given in rectangular, cylindrical and other geometries related to recent acquizition devices and techniques.
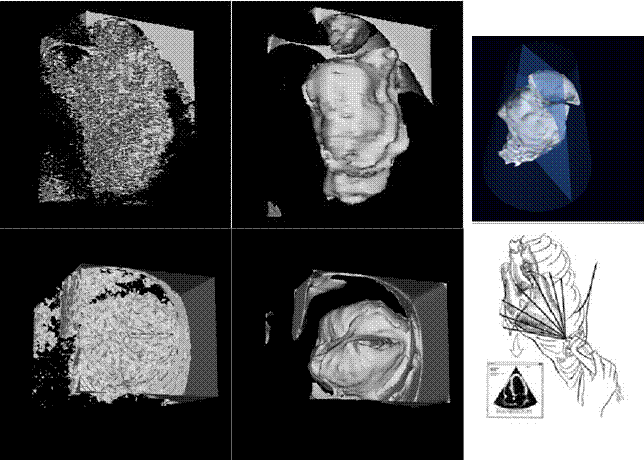
Denoised 3D images in cylindrical geometry
Recent image processing operations involving PDEs are nonlinear image filtration, edge detection, deblurring and image enhancement, restoration, image inpainting, shape extraction and analysis, image segmentation, motion analysis, motion based filtering etc.. Typical 2D examples are given by a large variety of medical images, satellite or camera system images, old archive documents, texts pre-processed for automatic reading, old corrupted photographs or any other digital images of poor quality. 3D examples arise in bioengineering, medicine or in material quality control, where 3D volumetric aquisition methods are widely used nowadays. The processing of image sequences can be found in the restoration of movies, video sequence analysis, visual recording of growth (of human organs, leaves of plants, etc.) or in improvement of the quality of medical image sequences. For example, the ultrasound acquisition of a beating heart in 3D echocardiography gives one such important application; the principal investigators of this project have long time experience in this field and they have made an important contributions to the topic (see [1]).
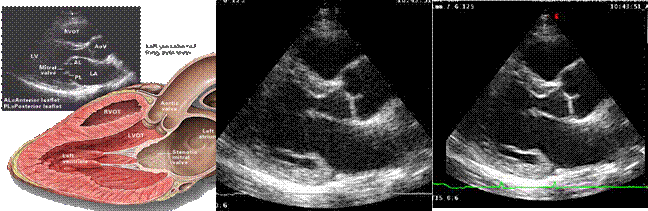
The multiscale analysis of 1st, 5th and 9th
time step of the echo-cardiographic sequence.
The shape of the left ventricle is extracted in those
moments of cardiac cycle.
From the mathematical point of view, the input processed image can be modelled by a real function u0(x), u0 : Ω → R, where Ω, a subset of Rd, represents a spatial domain. In the case of an input image sequence u0(x,θ), u0 : Ω x [0,TA]→ R, it depends on the additional parameter θ representing a point in a real time interval of acquisition [0,TA].
The first step to use PDEs for image processing was done in the beginning of eighties. By the simple observation that the Gauss function Gσ(x)=1/(4πσ)d/2 e-|x|^2/ (4σ) is a fundamental solution of the linear heat (diffusion) equation, it has been possible to replace the classical image processing operation - convolution of an image with Gσ with a given variance v=√(2σ) (Gaussian smoothing) - by solving the linear heat equation for a corresponding time t=σ with initial condition given by the processed image. It is well known that Gaussian smoothing (linear diffusion) blurs edges in the images and moves their positions. Although such a phenomenon can cause no problems in some examples of data analysis, in image processing, where the visual impression is important and a precise localization of edges is also necessary (e.g. to compute volumes of segmented objects), the linear image smoothing is generally not the best choice. A way has been found to overcome these shortcomings, namely to switch to nonlinear diffusion models. Due to the evolutionary character of the process which controls the processing using diffusion equations, application of any PDE to an initially given image is understood as its embedding in the so-called scale space. In the case of nonlinear PDEs one speaks about nonlinear scale space. The axioms and fundamental properties of such embeddings have been given and studied in [AGLM], where the notion of image multiscale analysis has been introduced. The image multiscale analysis associates with a given image u0(x) a family u(t,x) of smoothed-simplified images depending on an abstract parameter t in [0,T], the scale. As has been proved in [AGLM], if such a family fulfils certain basic assumptions - pyramidal structure, regularity and local comparison principle - then u(t,x) can be represented as the unique viscosity solution of a general second order (degenerate) parabolic partial differential equation. This theoretical result has also an important practical counterpart. The equations of (degenerate) parabolic type have a smoothing property, so they are a natural tool for filtering (image simplification) by removing spurious structures, e.g. noise. Moreover, the simplification should be image oriented, e.g. it should respect edges and not blur them. Or, it should recognize motion of a structure in an image sequence, and consequently the smoothing (diffusion) should respect the motion coherence in consecutive frames. Such requirements, or even more sophisticated ones related to the geometrical characteristics of the image, bring strong nonlinearity into the parabolic PDEs, and make this field interesting not only because of the applications but also from a mathematical and numerical point of view. Moreover, since image processing operations add further dimension to the problem (the scale space), e.g. in case of 3D+time sequences we have to solve computationally 5 dimensional problems, it is a chalenge for high scale and parallel computing facilities.
Since images are given on a discrete grid (pixel/voxel structure), we discretized the PDEs to get a numerical scheme implemented on the computer. The construction of fast and robust numerical schemes represents an important field of research, since the arising equations are higly nonlinear or even degenerate. Moreover one has to handle huge amount of data in fast and unconditionaly stable way. Semi-implicit schemes studied e.g. in [4,6,10], where the nonlinear terms of the equation are treated from the previous discrete scale step, and linear terms are considered at the current scale level, have favorable stability and efficiency properties. For space discretization either finite element method [4], finite/complementary volume method [6,10] or finite difference methods [CLMC,WRV] can be used. The finite element and finite/complementary volume methods are based on integral (weak, variational) formulations of the initial-boundary value problems for PDEs. Variational methods have a strong physical background since they are based on principles like minimization of energy (finite element method) or conservation laws (finite and complemetary volume methods). They allow a clear and physically meaningful derivation of difference equations which are local and easy to implement.
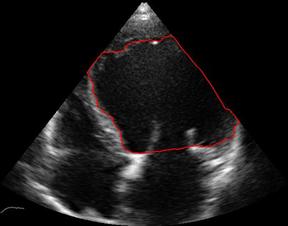
Original echo left ventricle (middle) and denoised (right) after 10 scale steps. Semi-implicit finite volume
During
this project we have developed new computational methods for the problems of
nonlinear image filtering and robust image segmentation for 2D, 3D images,
2D+time and 3D+time image sequences given in rectangular, cylindrical and other
nontrivial geometries related to recent acquizition devices and techniques. The
new numerical schemes will be studied regarding stability and efficiency of
computations as well as regarding the convergence to the weak solutions of the
corresponding PDEs. The discretized mathematical models have been based on
nontrivial generalizations of the nonlinear image selective smoothing equation
of the Perona-Malik type and on the morphologically invariant geometrical
equations of mean curvature flow type. The image sequences have been processed
and segmented using space and time coherence of moving structures. Preferably,
the robust semi-implicit time-scale discretizations, variational spatial
discretizations (adaptive finite element, finite/complementary volume methods)
and fast and robust linear algebra solvers have been used in order to achieve
fast and stable solutions.
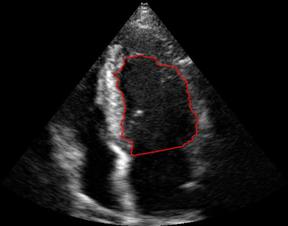
Left ventricle boundaries.
General References
[AGLM] L.Alvarez, F.Guichard, P.L.Lions, and J.-M.Morel, Axioms and fundamental equations of image processing, Arch. Rational Mech. Anal. 123(1993), 200--257.
[CLMC] F.Catté, P.L.Lions, J.-M.Morel, and T.Coll, Image selective smoothing and edge detection by nonlinear diffusion, SIAM J. Numer. Anal. 29 (1992), 182--193.
[WRV] J.Weickert, B.M.t.H.Romeny, M.A.Viergever, Efficient and reliable schemes for nonlinear diffusion filtering, IEEE Trans. Image Processing 7 (1998), 398--410.
Publications
[1] A. SARTI, K.MIKULA, F. SGALLARI Nonlinear multiscale analysis of three-dimensional echocardiographic sequences, IEEE Trans. Medical Imaging , Vol.18, No. 6, pp.453-466, 1999.
[2] A. SARTI, K.MIKULA, F. SGALLARI, C. LAMBERTI Nonlinear multiscale analysis models for filtering of 3D + time biomedical images, in "Geometric Methods in Bio-Medical image processing", R. Malladi, Ed., Lectures Notes Comput. Science and Eng., pp.107-127, Springer Verlag, 2002.
[3] A. SARTI, K.MIKULA, F. SGALLARI, C. LAMBERTI Evolutionary Partial Differential Equations for Medical Image Processing, Journal of Biomedical Informatics, pp. 77-91, Vol. 35, No. 2, April 2002.
[4] A. HANDLOVICOVA, K. MIKULA and F.SGALLARI, Variational numerical methods for solving nonlinear diffusion equations arising in image processing, Jour. Visual Communication and Image Representation, Vol.13, n1/2, pp.217-237, 2002.
[5] K. MIKULA, T. PREUSSER, M. RUMPF, F. SGALLARI On Anisotropic Diffusion in 3D image processing and image sequence analysis, in “Trends in Nonlinear Analysis”, (M.Kirkilionis, S. Kromker, R.Rannacher, F. Tomi (eds.), Springer Verlag, 2003, pp. 307-321.
[6] A. HANDLOVICOVA, K.MIKULA, F. SGALLARI, Semi-implicit complementary volume scheme for solving level set like equations in image processing and curvature evolution, Numerische. Mathematik., Vol.93, pp.675-695, 2003.
[7] K.MIKULA, F. SGALLARI, Semi-implicit finite volume scheme for image processing in 3D cylindrical geometry, Journ. Comp. Applied Mathem., Vol.161, pp.119-1325,2003.
[8] A. SARTI, K.MIKULA, F. SGALLARI, Co-volume level set method in subjective surface based medical image segmentation, in: Hand Book of Medical Image Analysis, Vol. I: Segmentation Models Part A(ed. by J.S. Suri, D.L.Wilson, S.Laxminarayan), KluwerAcademic/ Plenum publishers, New York, pp. 583-626, 2005.
[9] A. SARTI, K.MIKULA, F. SGALLARI, Co-volume method for Riemannian mean curvature flow in subjective surfaces multiscale segmentation, Computing and Visualization in Science, Vol. 9, pp. 23-31, 2006.
[10] S. CORSARO, A. SARTI, K.MIKULA, F. SGALLARI, Semi-implicit co-volume method in 3D image segmentation, SIAM Jour. Scient. Comput, Vol.28, No.6, pp. 2248-2265, 2006. With
Funded Projects
C.N.R. 2000-02 Strategic Project
"Numerical Methods for image and image sequences processing"
Coordinator Research Group University of Bologna: Prof. Fiorella Sgallari
NATO Project 2004 Reference : PST.CLG.979123
“Efficient and robust computational methods for biomedical image analysis”.
Scientific Coordinator: Prof. Fiorella Sgallari, University of Bologna.
Industrial Research Project:
“2D Segmentation of
Ultrasound Images”
Scientific Coordinator: Prof.
Fiorella Sgallari, University of Bologna.
(Esaote -Genova, TecnoBiomedica-Roma)
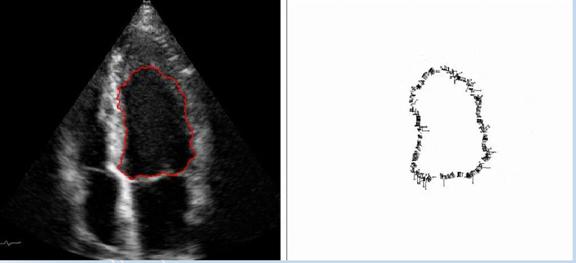
Segmentation and vector flow of left ventricle boundaries.
