Composed Segmentation and Reconstruction by an
Anisotropic PDE Model
Elena Franchini, Serena Morigi, Fiorella Sgallari
CIRAM – Dept. of Mathematics, University of Bologna, Italy
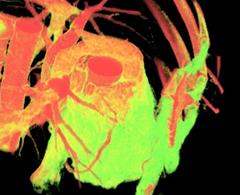
In this project we consider the problem of shape reconstruction from organized
and unorganized data set which has many important applications in medical
imaging, scientific computing, reverse engineering and geometric modelling. Most
of these applications rely on the efficient computation of partial differential
equations (PDE) on curves or surfaces implicitly represented by a level set
function.
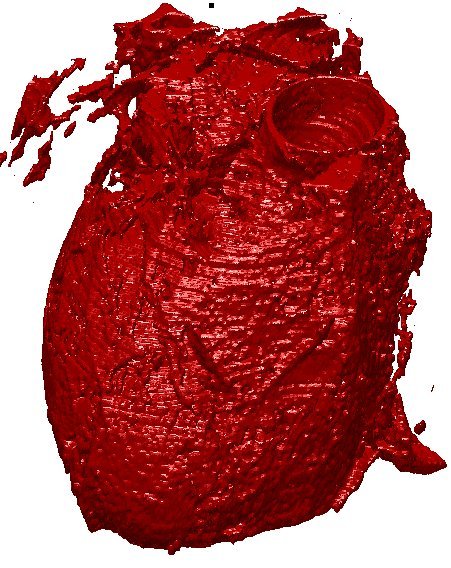
The advantages of these techniques are the topological flexibility, the possibility to easily capture geometry property of the surface, and to realize in a simple way the classical Boolean operations, while it is a challenge to deal with open or incomplete surfaces. In this work the reconstruction is obtained by continuously deforming an initial distance function following the PDE-based diffusion model derived from a minimal volume-like variational formulation. The gradient flow for this functional leads to a nonlinear curvature motion model. An anisotropic variant is provided which includes a diffusion tensor aimed to follow the object geometry and to deal with non-uniform and incomplete data set in order to construct an arbitrary topology surface with a controlled hole filling strategy.
|
(A) |
(B) |
|
(B)\(A) |
(B)\(A) |
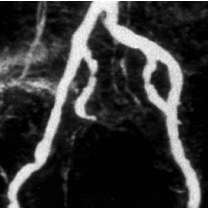
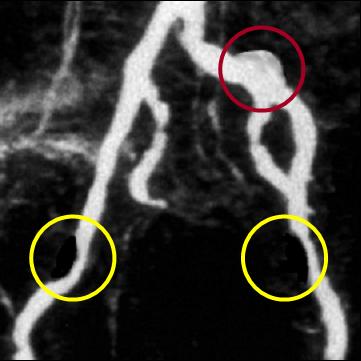
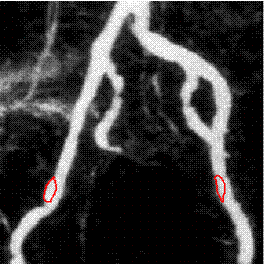
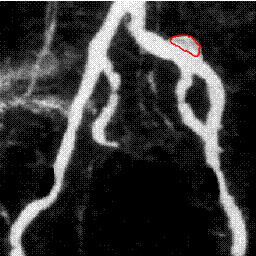
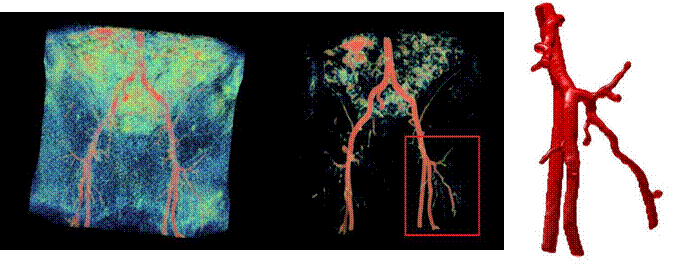
Moreover, we introduce the concept of composed segmentation (C-segmentation), that is a priori composition of sources to obtain a
single one segmentation result according to specific logic combinations. Numerical examples demonstrate the ability
of the proposed method to produce high quality 2D/3D reconstructions of complex and eventually incomplete synthetic and real data.
|
|
A U B |
|
(A) |
(B) |
[1] S. Morigi, L. Reichel and F. Sgallari, Composed Segmentation of Tubular Structures by an Anisotropic PDE Model, X.-C.Tai et al. (Eds): SSVM 2009, LNCS 5567, pp. 51-74, 2009, Springer-Verlag Berlin Heidelberg 2009.
[2] S. Morigi, L. Reichel and F. Sgallari, Implicit shape reconstruction of unorganized points using PDE-based deformable 3D manifolds. Numerical Mathematics: Theory, Methods and Applications ,( submitted) 2009.
