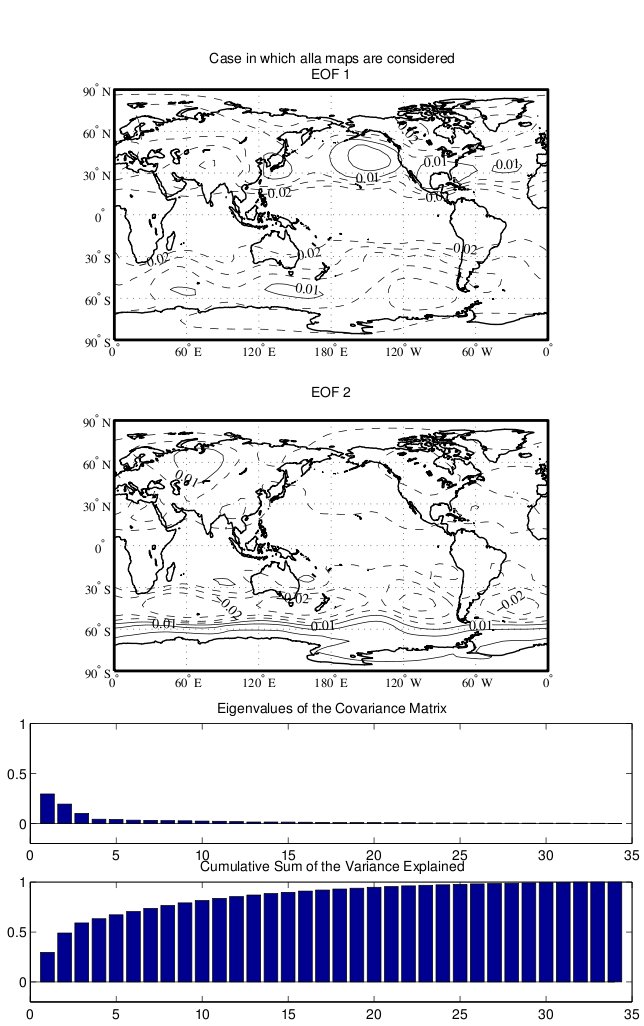
(seconda figura da: Navarra Simoncini, Springer 2010)

Matematica Computazionale:
Matrix methods for Data Science

a.a. 2024-2025. Corso opzionale della Laurea in Matematica (triennale) - Bologna
NOTA: Il corso e' fruibile anche dagli studenti delle Lauree Magistrali.

6 crediti
Lezioni: II semestre
Docente: Prof. V. Simoncini.
Modulo su laboratorio e Tensori: dott.ssa Martina Iannacito

Orari del Corso (inizio lezioni: 17/02/2025 )

Lun 9:00-11:00, Giovedi 9:00-11:00

Eventuali variazioni di orario saranno segnalate in fondo alla pagina.

Orario di Ricevimento Studenti

su appuntamento.

Programma

Il corso prevede lo studio di: Matrix methods for Data Science. L'informazione contenuta in grandi quantita' di dati, sfruttata per esempio dai motori di ricerca (es. Google), od usata nello studio di dati climatici, documenti, pattern e image recognition, ecc., e' spesso gestibile grazie all'uso di tecniche matriciali e tensoriali avanzate di alto livello, che sfruttino, per esempio, fattorizzazione opportune nell'ambito di problemi di ottimizzazione matriciali. Il corso prevede lo studio di queste tecniche, partendo dagli aspetti analitici di Teoria delle Matrici, e arrivando al loro utilizzo pratico in vari problemi benchmark nel Data Science.

Dettaglio

- Organizzazione dei dati e note introduttive
- Calcolo Matriciale: Autovalori e proprieta' variazionali
- Calcolo Matriciale: Valori singolari e loro proprieta'
- Calcolo tensoriale e HOSVD
- Applicazioni:
** Information retrieval in documenti mediante i problemi ai minimi quadrati
** Similarita', metodi di Clustering (Complete Linkage, kmeans, spectral clustering) e possibile cenno a metodi "randomized"
** Strategie matriciali per il Riconoscimento di Pattern/immagini
** Analisi delle Componenti Principali su osservazioni multivariate
** Strategie spettrali per il Page ranking
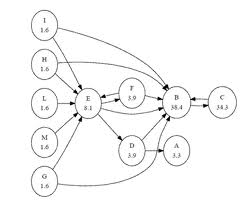
** Metodi matriciali per i complex networks
Applicazioni: (Handwritten digits, Text mining, Page Ranking)

Dettaglio: Registro delle lezioni completo del corso, a.a.2024-2025.

Il corso prevede 55 ore. L'attivita' didattica alternera' lezioni frontali (con lucidi) con applicazioni immediate al computer in ambiente Matlab con supervisione del docente, in cui gli studenti saranno incoraggiati ad implementare quanto appena visto a lezione. Il corso dell'a.a.2024-2025 prevede un Modulo Didattico sui Tensori, svolto dalla Dott.ssa Martina Iannacito.

Prerequisiti:

Concetti fondamentali di Analisi Matematica.
Algebra Lineare di base (spazi vettoriali, matrici, vettori, norma, ...) ed aspetti computazionali (QR, Choleski, LU, Autovalori, ...)
Conoscenze di base dell'ambiente computazionale Matlab.


Testi di Consultazione:


* Lucidi del corso (disponibili man mano che il corso procede). Sono possibili variazioni del materiale, quindi e' sconsigliata la stampa in anticipo rispetto alla lezione a cui si riferisce.
* Appunti di lezione di Virginia Nanni, a.a. 2024-2025 (forniti direttamente dall'autrice).
* Lezioni su Tensori a.a.2022-2023, per le lezioni sull'argomento, parte integrante del corso.

* R. Horn e C. Johnson, Matrix Analysis , Cambridge Univ. Press, 1985.
* Lars Elden, Matrix Methods in Data Mining and Pattern Recognition , SIAM, 2^ edizione, 2019.
*R. Johnson e D. Wichern, Applied Multivariate Statistical Analysis, Prentice-Hall, (V ed.) 2002. Dati relativi alle tabelle del libro.
* E. Estrada, The Structure of Complex Networks, Theory and Applications, Oxford Univ. Press, 2011.
* M.W. Berry and M. Browne, Understanding Search Engines: Mathematical Modeling and Text Retrieval , SIAM Book Series: Software, Environments, and Tools, Second Edition (Maggio 2005).
* Extrapolation Methods for Accelerating PageRank Computations Sep Kamvar, Taher Haveliwala, Chris Manning, and Gene Golub. Proceedings of the Twelfth International World Wide Web Conference, May, 2003.
* Algorithms for Non-negative Matrix Factorization Daniel D. Lee and H. Sebastian Seung, Advances in Neural Information Processing Systems 13, (2001), 556-562.
* Non-negative Matrix Factorization Nicolas Gillis, SIAM, 2020. Matlab software .
*Jingu Kim. Matlab software per non-negative matrix and tensor factorization
* Non-negative Matrix and Tensor Factorization. Applications to exploratory multi-way... A. Cichocki, R. Zdunek, A.~H. Phan and S.-i. Amari, Wiley, 2009.
* Algorithms, Initializations, and Convergence for the Nonnegative Matrix Factorization Russell Albright, James Cox, David Duling, Amy N. Langville, and Carl D. Meyer, NCSU Technical Report Math 81706.
* A tutorial on spectral clustering Ulrike von Luxburg, Statistics and COmputing, 17 (4), 2007.
* Spectral and Algebraic Graph Theory Incomplete Draft, dated December 4, 2019, Daniel A. Spielman, Yale University.
* Definizioni di funzione di matrice Nick Higham, estratto da "Functions of matrices, theory and computation", SIAM 2008.
* Network properties revealed through matrix functions Ernesto Estrada and Desmond J. Higham, SIAM Review, 52 (4), 2010.
* LSI Latent Semantic Indexing, sito di riferimento (non aggiornato di recente) Dataset per Inf Retr: Corpora/Glasgow Repository
* IR Information Retrieval Datasets
* Tensor Decompositions and Applications T. Kolda and B. Bader, SIAM Review, 51 (3), 2009.
* Capitolo sui Tensori, in "Matrix Computations", G. Golub and Ch. Van Loan, 4 Ed, (2013) Johns Hopkins Univ.Press.
* SVD and applications Z. Zhang, arXiv n.1510.08532v1 (2015).
* Randomly pivoted Cholesky: Practical approximation of a kernel matrix with few entry evaluations Y. Chen, E. Epperly, J. Tropp e R. Webber, arXiv 2207.06503v5 (2023)
  • The new frontier: Randomized Numerical Linear Algebra Scientific Machine Learning
    * Efficiency seminario del prof. L. De Angelis, UniBO, del 12 Aprile 2023.
    altri testi....

    * Funzioni per lezione su tensori. hosvd3.m , nmodeproduct.m , store_data.m , Dati: coil20.tar.gz, faces96.zip. Funzioni: svdtrunc_coil20.m , svdtrunc_faces96.m , svdtrunc_mnist.m
    Toolbox: tensor toolbox v.3.2.1 release v3.2.1, tensor toolbox v3.5 release attuale , tensor_toolbox-v3.5.tar --> vedi: Toolbox homepage, e la sezione "Functionality" per la documentazione.

    *

    Siti per dati:


    * Data from various sources.
    * UCI machine learning repository
    * SuiteSparse Matrix Collection
    * Data from TechTC (Technion Repository of Text Categorization Datasets) for text mining.
    * Software from TechTC (Technion Repository of Text Categorization Datasets)
    * Temporal Network repository



    Laboratorio Informatico:


    Esercizi del 27/02/25 Dati: zmi-geonode.png, query.png
    Esercizi del 06/03/25. Un possibile svolgimento . Dati: A_med.mat . Q_med.mat . dict_med.mat . Codice: lsqr.m
    Esercizi del 17/03/25. Dati: protein.m.
    Esercizi del 20/03/25. Dati: Esercizio 1: digits mnist_all.mat. Codici: ima2.m. Esercizio 2: faces96.zip, faces95.zip. codice testFace_U.m.
    Esercizi del 03/04/25. Dati: protein.m. clustering.m. Codice per le k-medie: test1_kmeans.m. Codice per Query allocation in information retrieval usando kmedie queries.m (dati da lucidi di lezione)
    Esercizi del 10/04/25. Dati: sample_orl.tar. get_matrices.m, orl_faces.tar.gz.
    Esercizi del 14/04/25. dati fisher
    Esercizi del 24/04/25. Dati: stanford-berkeley-web.tar.gz. non zippato: stanford-berkeley-web.tar.

    Prova d'esame:

    L'esame consiste in una prova orale che prevede due parti, svolte nella stessa sede: i) Risposte orali a domande sugli argomenti svolti a lezione; ii) Presentazione orale di un progetto su argomenti svolti nel corso e nel laboratorio informatico. (E' a disposizione un file (gzipped tar) con un esempio di semplice presentazione. Altri files utili: sem-page.sty. seminar.cls. Altrimenti si puo' usare il pacchetto beamer di latex.)

    Problemi per l'esame :

    testo.

    Link utili:

  • Arithmetic Formats for Machine Learning - Working group

    Informazioni utili:




    (Yale Face Dataset, http://vision.ucsd.edu/datasetsAll)