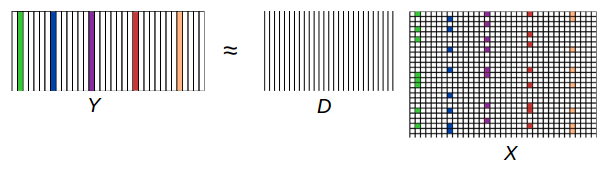

(ref.second image)
Matrix and Tensor methods for Data Science
a.y. 2024-2025
Course of the Curriculum
Advanced Mathematics for Applications, Master Degree in Mathematics - Bologna
6 CFU
Lectures: I semester (Part I, 40h).
Lecturer: Prof. V. Simoncini
Note: Part II (15h) lecturer prof. D. Palitta (Synopsis on Virtuale)
Time schedule Part I (25/09/2024- end of 11/2024)
Wednesday 14:00-16:00
Thursday 14:00-16:00
Please check at the bottom of this page for time changes.
Extra-class meeting time with students:
arrange meeting time by sending email to lecturer.
Aim
At the end of the course, students have theoretical and computational knowledge
on matrix and tensor techniques for analysing large amounts of data.
In particular, students are able to examine large samples of discrete data
and extract interpretable information of relevance in data processing stemming from
medical and scientific applications, and social and security sciences.
Part I.
The course presents fundamental matrix and tensor techniques commonly employed
in big-Data analysis methods, typically arising in data science, and which constitute
the technology for what is commonly called "machine learning".
Details:
* Vector and matrix norms (including sparsity promoting)
* Linear regression and multiple Least squares
* Eigenvalues, SVD, pseudoinverse
* Reduction and low rank representations
- PCA, factor analysis
- Sparse representation with l_0-norm
- Randomized techniques, CUR factorization
* Dictionary Learning
- Alternating direction methods, constrained optimization
* Tensors
- Dealing with tensors and various representations
- HOSVD, Tensor OMP, Dictionary Learning with tensors
Lectures lognotes , a.a.2024-2025, 40h (to be included at the end of the course).
Part I of the course consists of 40 hours,
alternating in presence lectures (with slides and "blackboard")
and computer sessions. The computational environment will be Matlab.
Requirements:
Basic concepts of mathematical analysis.
Numerical Linear Algebra (first course: norms, QR decomposition, Eig computations, direct and iterative system solvers, least squares and normal equation )
Intermediate knowledge of Matlab.
Computer lab sessions:
The course will include a significant number of computer lab hours, so that
the student can gain strong expertise with the computational methodology. The use of
a personal laptop is encouraged, however computers will also be made available.
Exam:
The final exam will consist of two parts:
1. Lab test (2h) based on the problems and
methods explored during the lectures and lab sessions.
2. Oral presentation (with slides)
of a take-home computational project (groups of at most 2 people per project).
Passing the lab test is a requirement, to proceed with the oral
presentation.
Tips:
Lab Test: As already mentioned, you can either use your laptop or the classrom PC with the help of a USB pen.
No wifi will be available during most of the exam.
Presentation: prepare a presentation with pdf slides of about 25-30 mins each, with reference to the project. Students working in pair should ensure that each person has enough material distinguished from the other.
If you like, you can refer to small parts of the code you have implemented, if you wish to describe some features of your code.
The code itself does not have to be shown during the presentation, but it should be available in case of questions.
References
* Course
Slides (available here as we move along).
* Handwritten notes on Virtuale, whenever performed
General References:
* R. Horn and C. Johnson, Matrix Analysis , Cambridge Univ. Press, 1985.
* G. Golub and C. van Loan, Matrix Computations , The Johns Hopkins University Press, 2013.
* Lars Elden,
Matrix Methods in Data Mining and Pattern Recognition , SIAM, 2^ ed., 2019.
*R. Johnson e D. Wichern, Applied Multivariate Statistical Analysis, Prentice-Hall, (V ed.) 2002.
Dati Tables in the book.
*
Numerical Optimization
J. Nocedal and S. J. Wright, 2006. For active set methods and other algorithms.
*
Optimization methods for large-scale machine learning.
Bottou, L., Curtis, F.E. and Nocedal, J., 2018.
SIAM review, 60(2), pp.223-311.
Low-rank and sparse representations:
*
SVD and applications
Z. Zhang, arXiv n.1510.08532v1 (2015).
*
From Sparse Solutions of Systems of Equations to Sparse Modeling of Signals and Images
Alfred M. Bruckstein, David L. Donoho, Michael Elad, SIAM Review, 51 (2009).
* Sparse-Plex
A journey into sparse and redundant representations. matlab and notebook.
Non-Negative factorization:
*
Algorithms for Non-negative Matrix Factorization
Daniel D. Lee and H. Sebastian Seung, Advances in Neural Information
Processing Systems 13, (2001), 556-562.
*
Non-negative Matrix Factorization
Nicolas Gillis, SIAM, 2020. Matlab
software .
*Jingu Kim. Matlab software for non-negative
matrix and tensor factorization
*
Non-negative Matrix and Tensor Factorization. Applications to exploratory multi-way...
A. Cichocki, R. Zdunek, A.~H. Phan and S.-i. Amari, Wiley, 2009. (Book,
currently not available)
*
Algorithms, Initializations, and Convergence for the Nonnegative
Matrix Factorization
Russell Albright, James Cox, David Duling, Amy N. Langville, and Carl D. Meyer,
NCSU Technical Report Math 81706.
-->
Factor Analysis:
* First
Varimax algorithm, Jennrich, Psychometrika, 2001.
Original
Varimax problem, Kaiser, 1958.
CUR:
*
article: "CUR matrix decompositions for improved data analysis",
M. Mahoney and P. Drineas, PNAS (2009).
*
article: "Improving CUR Matrix Decomposition and the Nystrom
Approximation via Adaptive Sampling", Shusen Wang, Zhihua Zhang, Journal of Machine Learning Research 14 (2013).
*
article:
Near-optimal column-based matrix reconstruction,
Christos Boutsidis, Petros Drineas, and Malik Magdon-Ismail
Dictionary learning:
*
Efficient Implementation of the K-SVD algorithm using Batch orthogonal matching pursuit
article by Rubinstein, M. Zibulevsky and Michale Elad, 2008 (related to the matlab code in the exercises)
Tensors:
*
Tensor Decompositions and Applications
T. Kolda and B. Bader, SIAM Review, 51 (3), 2009.
*
Chapter on Tensors, Matrix Computations, G. Golub and Ch. Van Loan, 4 Ed, (2013) Johns Hopkins Univ.Press.
*
Tensor dictionary learning with sparse TUCKER decomposition,
S. Zubair and W. Wang, in Proc. IEEE Int. Conf. Digit. Signal Process., 2013 (GradTensor).
*
Tensor-based algorithms for learning multidimensional separable dictionaries,
F. Roemer, G. D. Galdo, and M. Haardt,
in Proc. IEEE Int. Conf. Acoust. Speech Signal Process., 2014, pp. 3963-3967 (K-HOSVD).
 The new frontier:
Randomized Numerical Linear Algebra Scientific Machine Learning
The new frontier:
Randomized Numerical Linear Algebra Scientific Machine Learning
Software and Data:
*
CUR decomposition software (various algorithms)
*
Data from various sources.
*
UCI machine learning repository
* SuiteSparse Matrix Collection
*
Data from TechTC (Technion Repository of Text Categorization Datasets)
for text mining.
*
Software from TechTC (Technion Repository of Text Categorization Datasets)
tensor toolbox current release,
see: Toolbox homepage, and the "Functionality" section for
documentations.
Just in case: nmodeproduct.m .
* "An Introduction to Matlab 6.1"
, August 2001 (PDF format: 1500K, 35pp) by David F Griffiths with additional material by Ulf Carlsson,
Department of Vehicle Engineeering, KTH, Stockholm. Material updated for Matlab version 6.1.
Additional material will be included during the course.
Highlights:
 Arithmetic Formats for Machine Learning - Working group
Arithmetic Formats for Machine Learning - Working group
Computational exercises:
- Oct 2, 2024,
Text.
Data: rainCAL.dat.
- Oct 9, 2024,
Text.
Data: detroit.data.
- Oct 16, 2024,
Text.
Additional part of exercise.
Data: fashion_all.tar.gz.
Codes: codes_fashion.tar.gz.
Single files:
ex_omp_fashion.m .
loadMNISTImages.m .
loadMNISTLabels.m .
mp.m .
- Oct 24, 2024,
Text.
Data ex.1:
A_med.mat and
dict_med.mat.
Data ex.2: FX_March2010.
- Nov 07, 2024,
Text.
Data: glen_exp.tar.gz.
readfaces.m .
- Nov 14, 2024,
Codes for Dictionary Learning:
14112024.tar.gz.
Additional datasets: coil20.tar.gz;
yalefaces.tar.gz;
orl_faces.tar.gz.
Image plotting:
ima2.m (consider also using
Matlab function "imshow").
- Nov 21, 2024. Tensor reduction via HOSVD.
driver_hosvd.m, NOTE: the code requires the tensor toolbox (see above).
Dataset:
COIL-100.
- Nov 28, 2024. Image classification.
FaceRec_codes.tar.gz,
NOTE: the code requires the tensor toolbox (see above),
and uses the MNIST dataset
(mnist_all.mat).
Matlab codes for Tensor Dictionary Learning:
tensor_example.(zipped tar folder)
Exam dates:
15/01/2025, 9.00h (lab test) and 14:00h (presentation)
13/02/2025, 9.00h (lab test) and 14:00h (presentation)
Final Projects:
Possible Projects for the final exam.
Final Lab Test:
The student can select one between two texts provided at the beginning
of the test, on different topics.
Sample of possible lab texts:
Prototype A.
Prototype B.
Prototype C.
Prototype D.


