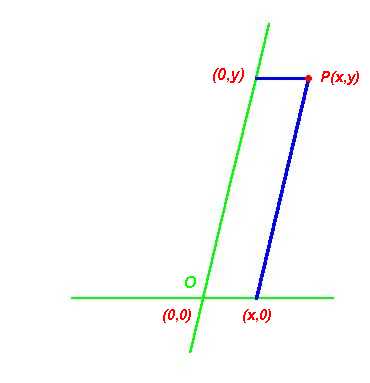
Nella geometria delle coordinate possiamo esprimere questa
costruzione geometrica definendo le coordinate della somma di due coppie di
numeri (cioè di due punti) come la somma delle coordinate corrispondenti
:
Qualunque sia il
punto
P, troviamo quindi che (x,y) =
(x,0)+(0,y) , e quindi ogni punto può essere espresso come somma di punti
degli assi
coordinati.
In questo sistema di coordinate, se scegliamo
gli assi coordinati perpendicolari tra loro , possiamo
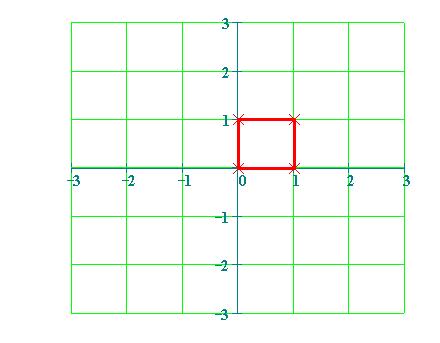
definire il quadrato unitario con i quattro vertici (0,0), (1,0), (1,1),
(0,1)
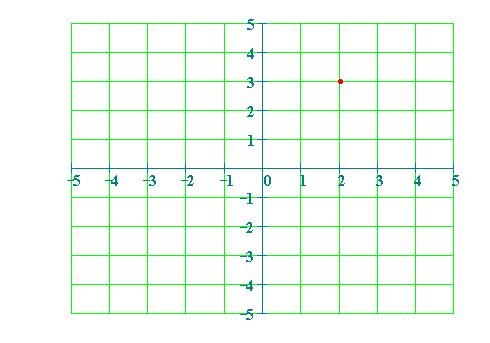
Rappresentiamo sul piano il punto P avente
ascissa x =
2 e ordinata y = 3 e
scriviamo P
(2,3) . Se scambiamo il valore dell'ascissa con quello dell'ordinata
otteniamo il punto Q (3,2)
.Facciamo variare il valore dell'ascissa, mantenendo costante l'ordinata:
osserveremo che il punto scorre, al variare dell'ascissa, sulla retta i cui
punti hanno tutti ordinata uguale a 3; si proceda analogamente facendo variare
l'ordinata e mantenendo costante l'ascissa oppure facendo variare l'ascissa x e
l'ordinata y in modo tale che
y = x, y =
-x,
assegnare ad x
valori compresi tra -5 e 5 e rappresentare , per esempio, i
punti Q ( , 3), R (
, 3), R (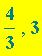 ), T
), T  , Z
, Z 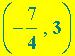
assegnare ad y
valori compresi tra -5 e 5 e rappresentare , per esempio, i
punti 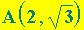 ,
, 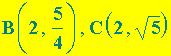
;
assegnare ad x e y
valori compresi tra -5 e 5 e rappresentare , per esempio,
alcuni punti per i quali risulta y = x o y = - x
Distanza
di due punti nel piano
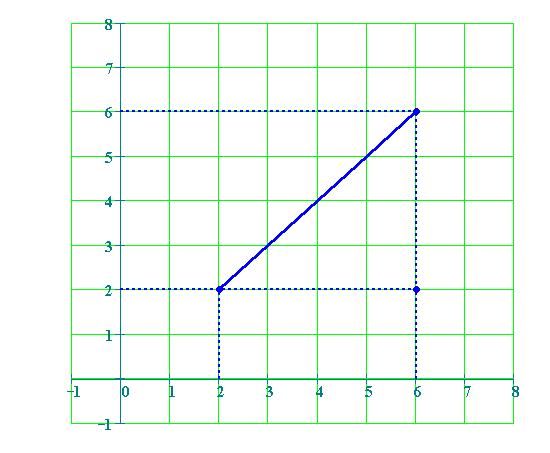
Siano
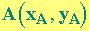
e
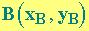
due punti del piano; per il teorema di Pitagora, la distanza di
A da B è data dalla formula
Se
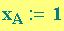
e
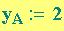
sono le coordinate del punto
A e
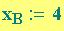
e
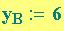
sono
le coordinate del punto
B la distanza tra i punti A e B è:
Poichè
il piano può essere pensato come un insieme di punti che sono in corrispondenza
biunivoca con coppie ordinate di numeri reali e su di esso, dati due punti A e
B, si può calcolare la loro distanza, esso
costituisce uno spazio bidimensionale e
metrico.
Geometria
delle coordinate
L'idea di base della geometria analitica, e che collega la
geometria all'algebra, è quella di identificare un punto dello spazio con una
sequenza ordinata di numeri. Renè
Descartes (Cartesio) pose le basi per lo
sviluppo della geometria delle coordinate e nel 1637 scrisse :" Ho applicato
l'algebra dei moderni alla geometria degli antichi e ho trovato così i
fondamenti di una scienza meravigliosa ". Assai prima di Cartesio ,
con le prime carte geografiche, era già nata implicitamente la geometria
analitica.
Il
metodo delle coordinate
Come
individuare la posizione di un punto sopra una retta, nel
piano?
- Su una retta
scegliamo un punto che assumiamo come origine O a cui assoceremo 0 e un
altro punto U (punto unitario) a cui sarà associato 1 .
L'origine è il punto di partenza, la distanza tra l'origine e il punto
unitario stabilisce una scala sulla nostra retta. Ogni punto della semiretta
che contiene il punto 1 può essere individuato tramite la sua distanza
dall'origine, rappresentata come multiplo della distanza tra 0 e 1; se un
punto sta sulla semiretta opposta, sarà individuato dalla sua distanza da 0,
questa volta preceduta da un segno negativo.
In questo modo è stato scelto sulla retta un riferimento
cartesiano e la retta è denominata
retta cartesiana.
Si può perciò dire che ogni punto
corrisponde a un numero reale, che è la sua
coordinata
(possiamo denominarla ascissa
), e viceversa ogni numero
reale corrisponde a un punto.
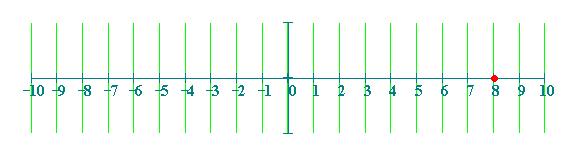
Rappresentiamo sulla retta il punto P avente ascissa x = 8 e
scriviamo P
(8) . Facciamo variare il valore dell'ascissa: osserveremo che il punto
scorre sulla retta al variare dell'ascissa ed potrà essere situato alla destra
di O oppure alla sinistra di O o coincidere con O.
assegnare ad x
valori compresi tra -10 e 10 e rappresentare , per esempio, i
punti Q
( 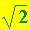 ), R (
), R (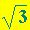 ), T (
), T (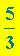 ), Z (
), Z (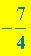 )
)
Distanza
tra due punti di una retta cartesiana
Siano
P (x1) e
Q (x2) due punti
della retta cartesiana r. Definiamo distanza di P da Q , e scriviamo
d(P,Q), il
valore assoluto
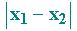
, in simboli:
d(P,Q)= 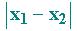
x 1= 5 e x 2 = 3 sono
le ascisse dei punti P e Q
assegnare ad
x1 e x2 altri valori
reali e sarà di
conseguenza calcolata la distanza tra i due punti
Poichè
la retta può essere pensata come un insieme di punti che sono in corrispondenza
biunivoca con i numeri reali e su di essa, dati due punti P e Q, si può
calcolare la loro distanza, essa costituisce
uno spazio unidimensionale e
metrico.
-
Per stabilire le
coordinate dei punti del piano ,
prendiamo in primo luogo due rette cartesiane non parallele, chiamate assi
coordinati. Il punto in cui si incontrano, che chiameremo origine, sarà
individuato dalla coppia (0,0) ;
-
i punti del primo asse saranno associati alle coppie (x,0)
;
-
i punti del secondo asse alle coppie (0,y);
-
dato ora un punto P
qualsiasi del piano, possiamo tracciare le parallele agli assi coordinati che
passano per quel punto e che incontreranno il primo asse in un punto del tipo
(x,0) ,
il secondo asse in un punto del tipo (0,y);
-
la posizione del punto rispetto agli assi coordinati che
abbiamo scelto è determinata dalla coppia di numeri (x,y) ;
x è
detta ascissa,
y è
l'ordinata;
i l punto (x,y) è il quarto vertice di un parallelogramma che ha un
vertice nell'origine e gli altri vertici in (x,0) e
(0,y).
 , Z
, Z 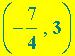
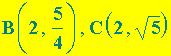 ;
; 
![]()
![]()
![]()