

Abbiamo considerato il caso di tre eventi E 1, E 2, E3 con l'evento E3 logicamente semidipendente o dipendente dagli eventi E1e E 2. Gli eventi E 1 e E 2 possono, nei vari casi considerati, essere o meno logicamente indipendenti fra loro. Consideriamo i loro otto costituenti:
Q0
= E1~E
2~ E3
~
Q1
= E1E2~
E3~
Q2
= E1~E2
E3~
Q3 = E1
~
E2~ E
3
Q1
' = E1~E
2 E3
Q2
' = E1
E2~E
3
Q3
'= E1
E2E3
~
Q0
' = E1
E2
E3
Qui identifichiamo gli eventi con numeri aleatori che assumono valori 1 se si verificano e 0 altrimenti; il prodotto di eventi corrisponde quindi all'intersezione nell'usuale interpretazione insiemistica, mentre E = 1-E denota l'evento complementare di E. Ai costituenti facciamo corrispondere i punti che corrispondono ai valori corrispondenti di (E1, E 2, E3):
(0, 0, 0) (1, 0, 0) (0, 1, 0) (0, 0, 1)
(0, 1, 1) (1, 0, 1) (1, 1, 0) (1, 1, 1).
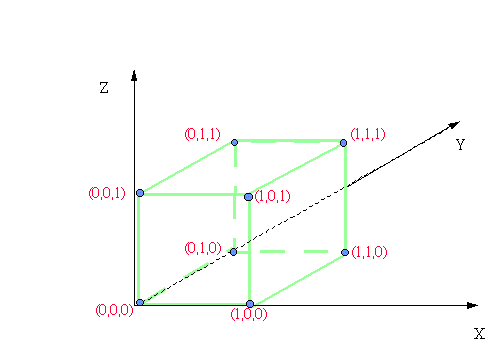
Data la relazione di semidipendenza o dipendenza logica di E3 con E1 e E2 non tutti i costituenti sono possibili. Nel disegno viene evidenziato nei vari casi l'involucro convesso dell'insieme dei punti possibili all'interno del cubo unitario. L'utente può indicare due possibili valori per le probabilità P (E1)e P(E2) e, cliccando sul primo bottone che reca scritto traccia, il programma fa apparire il segmento unitario intersezione della retta parallela al terzo asse per il punto (P(E1 ), P (E2), 0)con evidenziato il segmento intersezione con l'involucro convesso dei punti possibili che rappresenta quali sono i valori per P (E3) compatibili con l'assegnazione di P(E 1), P( E2). Nel caso in cui E1ed E2 non sono logicamente indipendenti fra loro, se l'assegnazione di P(E 1), P(E2) non e' compatibile, questo viene comunicato con un messaggio e quindi l'esecuzione si blocca. Riportiamo alcune immagini relative a vari casi considerati. Nella realizzazione il cubo, l'involucro convesso dei punti possibili, il segmento e la sua intersezione appaiono in colori diversi.