


Next: About this document ...
Up: Curriculum dell' attivitá didattica
Previous: Attivitá didattica
Nella mia attivitá scientifica mi sono occupato, a grandi linee, di
1) teoria dell'interpolazione;
2) equazioni differenziali ordinarie in spazi vettoriali topologici
(soprattutto di Banach), con applicazioni a problemi misti per equazioni
a derivate parziali;
3) problemi misti per equazioni paraboliche;
4) problemi al contorno ellittici;
5) equazioni di convoluzione astratte con applicazioni a problemi ellittici
con condizioni al contorno di tipo dinamico;
6) equazioni integrodifferenziali di Volterra di tipo parabolico;
7) operatori differenziali in spazi di funzioni piatte;
8) discretizzazione con metodi alle differenze finite di problemi al contorno
ellittici e problemi misti parabolici.
Passo ora in rassegna le mie pubblicazioni:
1) Some properties of the sum and the intersection of normed spaces
con G. Dore e A. Venni in Atti Sem. Mat. Univ. Modena, XXXI, 325-331, 1982.
Si studiano alcune proprietá della somma e dell' intersezione di spazi normati.
Si danno inoltre due controesempi alla seguente
(apparentemente ragionevole) congettura: se X é uno spazio normato immerso
con continuitá in A0 e in A1 e denso in ciascuno di essi, allora X
é denso in
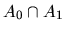 .
Il contributo dei tre autori é stato sostanzialmente paritetico. Mio é il controesempio
3.1.
2) Complex interpolation for 2N Banach spaces, con G. Dore e A. Venni
in Rend. Sem. Mat. Univ. Padova, vol. 76, 1-36, 1986.
Questo lavoro costituisce un tentativo di estendere il classico metodo di
interpolazione complesso a un numero di spazi superiore a 2.
Si considera una famiglia (Aj) di 2N spazi di Banach compatibili.
Per
.
Il contributo dei tre autori é stato sostanzialmente paritetico. Mio é il controesempio
3.1.
2) Complex interpolation for 2N Banach spaces, con G. Dore e A. Venni
in Rend. Sem. Mat. Univ. Padova, vol. 76, 1-36, 1986.
Questo lavoro costituisce un tentativo di estendere il classico metodo di
interpolazione complesso a un numero di spazi superiore a 2.
Si considera una famiglia (Aj) di 2N spazi di Banach compatibili.
Per 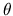 in ]0, 1[N si definisce un certo spazio
in ]0, 1[N si definisce un certo spazio 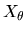 in modo tale
che, se N = 1, si ottiene il solito spazio di interpolazione complesso.
Si estendono parecchie proprietá note nel caso N = 1, in particolare la
proprietá di interpolazione e, parzialmente, la proprietá di reiterazione.
Il contributo dei tre autori é stato sostanzialmente paritetico.
3) Strongly continuous semigroups, weak solutions and the variation of
parameter formula in locally convex spaces, Boll. U. M. I. Anal. Funz. Appl.,
ser. VI, vol. IV-C, n. 1, 431-440, 1985.
Si dá un'estensione al caso degli spazi vettoriali topologici di un risultato,
dovuto a J. M. Ball nel caso degli spazi di Banach, sulla buona posizione in
un certo senso debole del
problema di Cauchy astratto
in modo tale
che, se N = 1, si ottiene il solito spazio di interpolazione complesso.
Si estendono parecchie proprietá note nel caso N = 1, in particolare la
proprietá di interpolazione e, parzialmente, la proprietá di reiterazione.
Il contributo dei tre autori é stato sostanzialmente paritetico.
3) Strongly continuous semigroups, weak solutions and the variation of
parameter formula in locally convex spaces, Boll. U. M. I. Anal. Funz. Appl.,
ser. VI, vol. IV-C, n. 1, 431-440, 1985.
Si dá un'estensione al caso degli spazi vettoriali topologici di un risultato,
dovuto a J. M. Ball nel caso degli spazi di Banach, sulla buona posizione in
un certo senso debole del
problema di Cauchy astratto
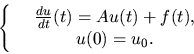 |
(1) |
Si introduce inoltre una versione generalizzata della formula di variazione
delle costanti.
4) On a singular evolution equation in Banach spaces,
con G. Dore, in
"Differential equations in Banach spaces (ed. A. Favini, E. O-
brecht), Springer
Lecture Notes in Mathematics 1223, 1986.
Si studia l'equazione differenziale astratta
senza condizioni iniziali nel caso in cui gli operatori
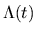 siano,
essenzialmente, generatori infinitesimali di semigruppi analitici in un certo
spazio di Banach e il dominio di
siano,
essenzialmente, generatori infinitesimali di semigruppi analitici in un certo
spazio di Banach e il dominio di
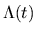 sia indipendente da t. Si
provano risultati di esistenza e unicitá di soluzioni di classe Ck nella
variabile t su tutto [0, T]. Si studia infine l'unicitá della soluzione
intesa in un certo senso debole. I risultati sono applicabili a problemi parabolici
singolari, con condizioni al contorno indipendenti da t.
Il contributo dei due autori é stato sostanzialmente paritetico.
5) Linear singular parabolic equations in Banach spaces,
in Math. Zeit. 195, 487-504, 1987.
Si continua lo studio iniziato nel lavoro precedente, trattando il caso in cui
il dominio di
sia indipendente da t. Si
provano risultati di esistenza e unicitá di soluzioni di classe Ck nella
variabile t su tutto [0, T]. Si studia infine l'unicitá della soluzione
intesa in un certo senso debole. I risultati sono applicabili a problemi parabolici
singolari, con condizioni al contorno indipendenti da t.
Il contributo dei due autori é stato sostanzialmente paritetico.
5) Linear singular parabolic equations in Banach spaces,
in Math. Zeit. 195, 487-504, 1987.
Si continua lo studio iniziato nel lavoro precedente, trattando il caso in cui
il dominio di
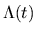 dipende da t. Naturalmente in questo caso i
risultati ottenuti sono applicabili a problemi parabolici concreti con
condizioni al contorno dipendenti da t.
6) On the asymptotic behavior of solutions of linear nonautonomous parabolic
equation, Boll. U. M. I. (7) 1-B, 1055-1076 (1987)
Si danno condizioni sufficienti per la convergenza a uno stadio stazionario per
dipende da t. Naturalmente in questo caso i
risultati ottenuti sono applicabili a problemi parabolici concreti con
condizioni al contorno dipendenti da t.
6) On the asymptotic behavior of solutions of linear nonautonomous parabolic
equation, Boll. U. M. I. (7) 1-B, 1055-1076 (1987)
Si danno condizioni sufficienti per la convergenza a uno stadio stazionario per
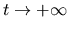 delle soluzioni del problema
delle soluzioni del problema
nel caso in cui gli operatori A(t) siano generatori infinitesimali di semigruppi
analitici. Il dominio di A(t) puó variare con t. Ció permette di
generalizzare alcuni risultati di Tanabe e Pazy, in cui si supponeva il
dominio di A(t) costante. Si considera anche il caso in cui A(t) ammetta
un certo sviluppo asintotico per
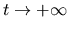 e si ricava un corrispondente
sviluppo asintotico per u(t).
I risultati di questo lavoro sono stati utilizzati in seguito da Tanabe e Park
per trattare il comportamento asintotico di soluzioni di equazioni paraboliche
in L1 (vedi Ann. Sc. Norm. Sup. Pisa, ser. IV, vol. XIV, 587-612 (1987)).
7) Convergence to a stationary state and stability for solutions of
quasilinear parabolic equations,
Ann. Mat. Pura Appl., IV, vol. CLI, 331-358
(1988).
Si danno risultati di stabilitá e di stabilitá asintotica per le soluzioni
del problema parabolico quasi lineare astratto
e si ricava un corrispondente
sviluppo asintotico per u(t).
I risultati di questo lavoro sono stati utilizzati in seguito da Tanabe e Park
per trattare il comportamento asintotico di soluzioni di equazioni paraboliche
in L1 (vedi Ann. Sc. Norm. Sup. Pisa, ser. IV, vol. XIV, 587-612 (1987)).
7) Convergence to a stationary state and stability for solutions of
quasilinear parabolic equations,
Ann. Mat. Pura Appl., IV, vol. CLI, 331-358
(1988).
Si danno risultati di stabilitá e di stabilitá asintotica per le soluzioni
del problema parabolico quasi lineare astratto
I risultati astratti sono applicati a problemi del tipo
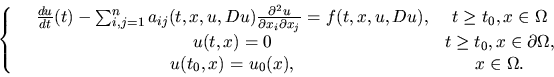 |
(2) |
con 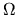 aperto regolare in
aperto regolare in 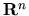 e
e
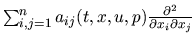 ellittico.
La sezione finale contiene un risultato di esistenza di una varietá stabile
ottenuto anche (independentemente) da G. Da Prato e A. Lunardi (vedi Arch. Rat.
Mech. Anal., vol. 101, n. 2, 115-142 (1988)).
8) On certain semigroups of linear operators and generalized Cauchy problem,
Osaka Math. Jour., 26, 89-118 (1989).
Si studia la generazione di semigruppi analitici in certi spazi non normabili
di distribuzioni su
ellittico.
La sezione finale contiene un risultato di esistenza di una varietá stabile
ottenuto anche (independentemente) da G. Da Prato e A. Lunardi (vedi Arch. Rat.
Mech. Anal., vol. 101, n. 2, 115-142 (1988)).
8) On certain semigroups of linear operators and generalized Cauchy problem,
Osaka Math. Jour., 26, 89-118 (1989).
Si studia la generazione di semigruppi analitici in certi spazi non normabili
di distribuzioni su 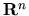 da parte di sistemi ellittici nel senso di
Petrovskii. Tali risultati si applicano ad alcuni semplici sistemi di tipo
ultraparabolico che intervengono in biologia. Si considerano, in particolare,
certi spazi di funzioni continue con peso in cui si ha generazione di un
semigruppo
da parte di sistemi ellittici nel senso di
Petrovskii. Tali risultati si applicano ad alcuni semplici sistemi di tipo
ultraparabolico che intervengono in biologia. Si considerano, in particolare,
certi spazi di funzioni continue con peso in cui si ha generazione di un
semigruppo 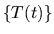 analitico ma non quasi equicontinuo (tale cioé che non esiste
alcun
analitico ma non quasi equicontinuo (tale cioé che non esiste
alcun
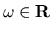 tale che
tale che
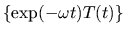 sia
equicontinuo). Si vede invece, che sotto opportune maggiorazioni dei coefficienti,
si ha generazione di un semigruppo quasi equicontinuo nello spazio delle
distribuzioni temperate. In questo caso il semigruppo possiede molte delle
proprietá "standard" dei semigruppi analitici negli spazi di Banach.
9) A maximal regularity result with applications to parabolic problems
with nonhomogeneous boundary conditions,
Rend. Sem. Mat. Univ. Padova, vol. 84, 1-37, 1990.
Si considera il generico problema misto parabolico "autonomo"
sia
equicontinuo). Si vede invece, che sotto opportune maggiorazioni dei coefficienti,
si ha generazione di un semigruppo quasi equicontinuo nello spazio delle
distribuzioni temperate. In questo caso il semigruppo possiede molte delle
proprietá "standard" dei semigruppi analitici negli spazi di Banach.
9) A maximal regularity result with applications to parabolic problems
with nonhomogeneous boundary conditions,
Rend. Sem. Mat. Univ. Padova, vol. 84, 1-37, 1990.
Si considera il generico problema misto parabolico "autonomo"
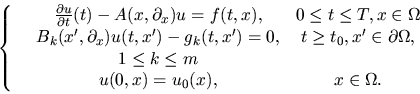 |
(3) |
con
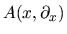 propriamente ellittico di ordine 2m e, per
propriamente ellittico di ordine 2m e, per
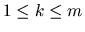 ,
i
,
i
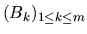 tali che sia soddisfatta la condizione di Lopatinskii.
Si prova un risultato di regolaritá massimale nello spazio
tali che sia soddisfatta la condizione di Lopatinskii.
Si prova un risultato di regolaritá massimale nello spazio
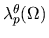 con
con
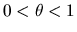 e
e
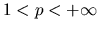 .
Tale spazio si definisce
come
.
Tale spazio si definisce
come
con
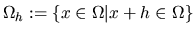 .
Il risultato é poi esteso ai casi
non autonomo e quasi lineare.
10) On elliptic problem in Besov spaces , Math. Nacht. 152, 247-275, 1991.
Si studia la risolubilitá del problema ellittico
.
Il risultato é poi esteso ai casi
non autonomo e quasi lineare.
10) On elliptic problem in Besov spaces , Math. Nacht. 152, 247-275, 1991.
Si studia la risolubilitá del problema ellittico
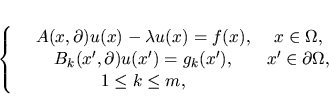 |
(4) |
con 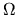 aperto regolare in
aperto regolare in 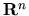 ,
,
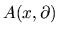 propriamente
ellittico
di ordine 2m,
propriamente
ellittico
di ordine 2m,
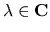 ,
f nello spazio di Besov
,
f nello spazio di Besov
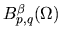 (
(
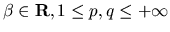 )
e, se l'ordine di Bk é mk,
)
e, se l'ordine di Bk é mk,
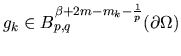 ,
,
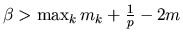 .
. Si prova che,
sotto opportune ipotesi, il problema
(
.
. Si prova che,
sotto opportune ipotesi, il problema
(![[*]](/usr/local/latex2html/icons.gif/cross_ref_motif.gif) ) ha un'unica soluzione nello spazio di Besov
) ha un'unica soluzione nello spazio di Besov
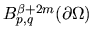 e si determinano stime ottimali della soluzione
in funzione del parametro
e si determinano stime ottimali della soluzione
in funzione del parametro  .
In certi casi si ottengono stime che
permettono di provare la generazione di un semigruppo analitico, non
fortemente continuo in 0 se
.
In certi casi si ottengono stime che
permettono di provare la generazione di un semigruppo analitico, non
fortemente continuo in 0 se
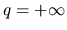 .
.



Next: About this document ...
Up: Curriculum dell' attivitá didattica
Previous: Attivitá didattica
Davide Guidetti
2000-04-12
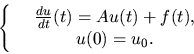
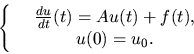
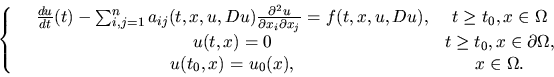
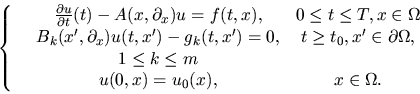
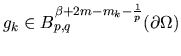 ,
,