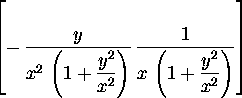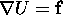Sia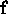 
un campo vettoriale differenziabile con continuità: una funzione U di classe 
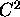si dice potenziale di f se 
. ,
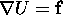Se f è una lista di m vettori (funzione vettoriale) e v una lista di n variabili, il comando potential(f,v,'U')
determina U se f ammette potenziale: la risposta è true (false) se U esiste (non esiste), e la successiva richiesta (se la risposta è stata true) fornisce il potenziale U.
> g:=[3*x^2*y-y^2,x^3-2*x*y+1];
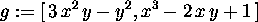
> potential(g,[x,y],'U');
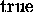
> U;
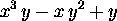
E` interessante il seguente esempio:
> with(linalg);
> f:=[-y/(x^2+y^2),x/(x^2+y^2)];
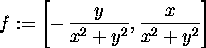
> v:=[x,y];
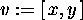
> jacobian(f,v);
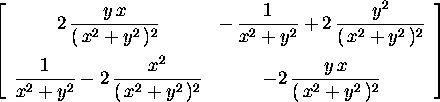
> diverge(f,v);
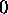
> potential(f,v,'U');
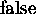
> g:=arctan(y/x);
> grad(g,v);
