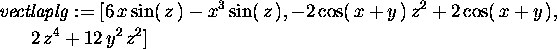Sia f una funzione scalare f di classe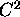 
: laplaciano di f è l'espressione
Assegnata un espressione scalare f e una lista di variabili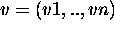 
,
il comando
laplacian(f ,v)
calcola la somma dei termini diff(f(v), vi$2).
Si noti il risultato dei seguenti due comandi.
> lap(f):=laplacian(f(x,y,z),[x,y,z]);
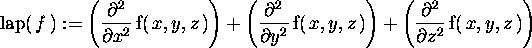
> A:=diverge(grad(f(x,y,z),v),v);
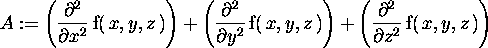
> evalb(lap(f)=A);
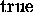
Ciò significa che
Rileviamo che il comando evalb(a,b) valuta l'eguaglianza booleana tra a e b.
Calcoliamo lo jacobiano di un gradiente e rileviamo che la sua traccia dà il laplaciano di f.
> J:=jacobian(grad(f(x,y,z),v),v);
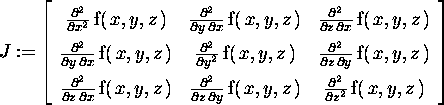
> trace(J);
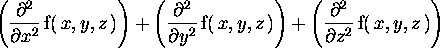
Assegnato una lista di espressioni f=(f1,f2,f3) e la lista di variabili v=(v1,v2,v3), il comando map(laplacian,f,v)
fornisce il vettore che ha per componenti i laplaciani delle componenti.
> g(x,y,z):=[x^3*sin(z),cos(x+y)*z^2,y^2*z^4];
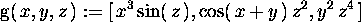
> vectlaplg:=map(laplacian,g(x,y,z),v);
