Image interpolation is of great importance in biomedical visualization and analysis. Most 3D biomedical volume images are sampled anisotropically, with the distance between consecutive slices significantly greater than the in-plane pixel size.
Image interpolation creates a number of new slices between known slices in order to obtain an isotropic volume image. From this volume image the 3D object of interest is then reconstruct. A major application of multidimensional image interpolation is the three-dimensional reconstruction of bone geometry and tissue density features starting from non-invasive measures, such as computerized tomography. In computerized tomography a bone, or other 3D objects of interest, can be reconstructed from a series of two dimensional (2D) parallel slices. Situations where these reconstructions are needed include: prosthesis design, surgery planning. It is also used in the 3D visualization of anatomy for purposes of investigating the structural and functional behaviours of human bones, this being accomplished by finite-element modelling.
During in-vivo CT data acquisition, the number of scans must be limited in order to protect patients from the risks related to X-ray absorption. Since the 3D reconstruction accuracy depends on which set of image slices are used in the reconstruction process the first problem to cope with is to define the location of a set of image slices which lead to optimal 3D reconstruction.
The main goal in this process is then maximize the density of information, minimizing the X-ray absorption.
In clinical practice the position of the CT scans is decided by the radiologists on the basis of an X-ray anterior-posterior projection of the bone segment under examination (the so-called scout image). In order to solve this first problem, this work will present a heuristic method to detect a subset of slices that leads to a pseudo-optimal 3D reconstruction of the bone.
The second problem is the choice of an image interpolation method to finalize the reconstruction of the missing slices.
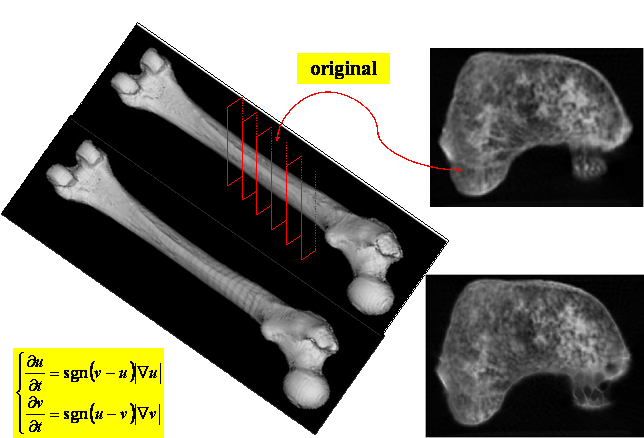
In this work we present a new approach for the image interpolation problem which, while retaining important features of the existing methods, overcomes most of their limitations. Our method is based on the level set ideas developed by Osher and Sethian, which has been proved powerful in front tracking, and it has recently been adopted in many image processing applications. The front is a closed, nonintersecting, hypersurface flowing along its gradient field with either constant speed, or a speed that depends on the curvature. The motion of the front is given by solving a "Hamilton-Jacobi" type equation written for a function in which the front is a particular level set.
Partial Differential Equations (PDE) models have recently emerged in image processing as an alternative to traditional approaches.
The preliminary results we have obtained investigating the use of a PDE approach to the image interpolation and reconstruction problem was promising and this has "encouraged" us to finalize a suitable PDE model for this interesting problem.
We adopt the level set technique for representing feature shapes in cross sections of the object that has to be reconstructed, then we follow the propagation of these shapes between given slices. In general, we do not have any a priori knowledge about the topology of the structures of the shape to be reconstructed. Among other advantages, the level set approach handles naturally the topological changes in the evolving level set curves. Thus the method can be successfully applied to data set containing tree anatomical structures.
A similar philosophy, in a discrete setting, has been followed by the shape-based method, which is one of the most popular among the methods for image interpolation.
In this work, we reformulate the shape-based method as an interface propagation problem. This leads us to an intuitive comprehension of the differences with our proposal.
The proposed interpolation algorithm has been tested successfully to CT images for a long bone reconstruction case study, although it could be easily applied to different kind of medical images, such as Positron Emission Tomography (PET) and Magnetic Resonance (MR) images.
We should note that all the CT images we analysed for the experimental tests present a very low noise level as we can observe from the images reported later in this work which did not require a pre-filtered step.
Obviously, for processing noisy images, such as ultrasound images, a denoising pre-filtering step is essential in order to avoid numerical problems arising from derivative calculations.
However, since the PDE level set approaches, as it is well known, are well suited to denoise medical images, a more general model could be developped in order to integrate a denoising operator in the reconstruction model we propose.
![]()
S.Morigi, F.Sgallari, C.Zannoni, A.Cappello An anisotropic nonlinear diffusion approach to image interpolation, Proceeding Conf. MTNS 2000, France, 2000.
S.Morigi, F.Sgallari 3D long bones reconstruction based on level sets, 2003