Valeria Simoncini. Research Interests and Problem Solving
Research Interests: Matrix Computations in Science and Engineering
Problem Solving:
Development and analysis of efficient solution strategies for large algebraic linear systems: symmetric and nonsymmetric
systems stemming from FD, FE, etc methods for elliptic PDEs
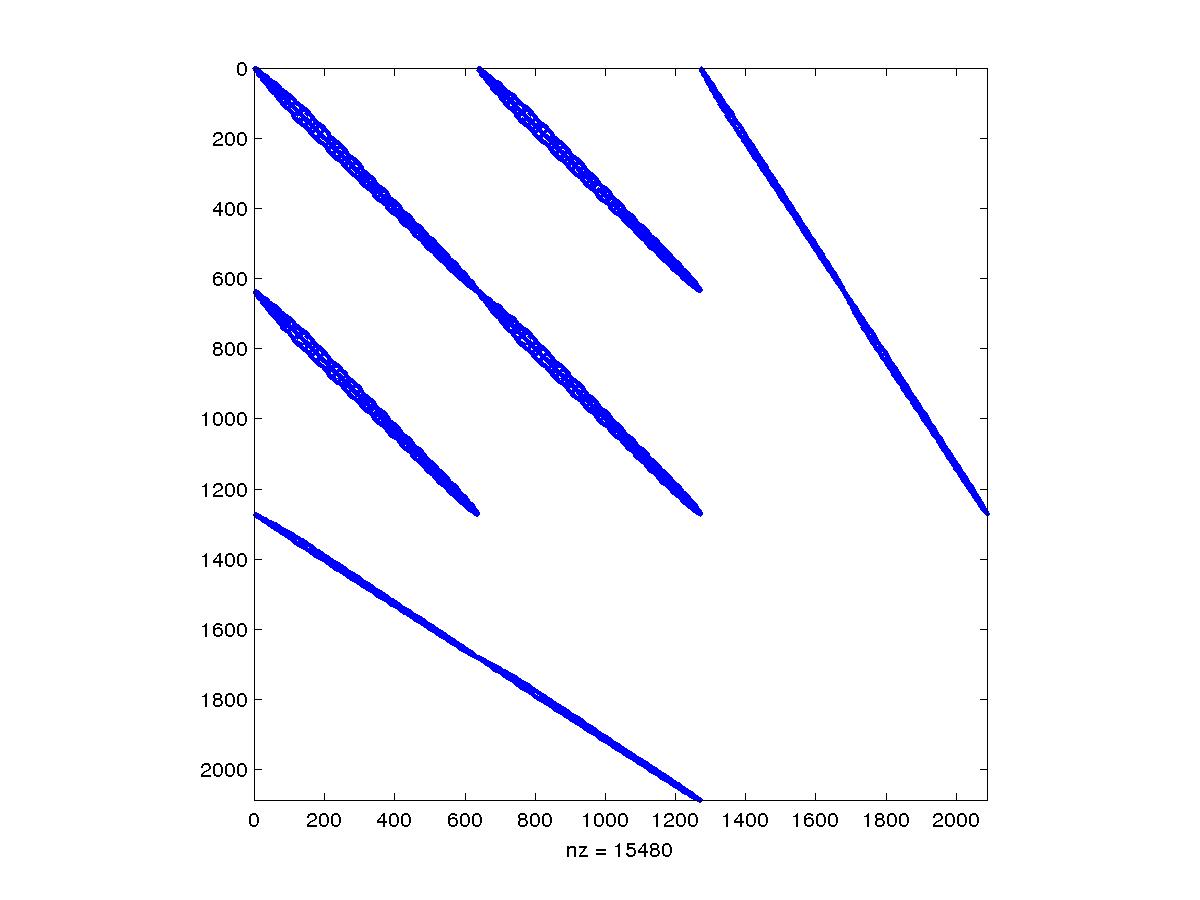 Saddle point problems from (PDE-)Constrained Optimization, Mixed formulations, etc. (for the plot see [3])
Saddle point problems from (PDE-)Constrained Optimization, Mixed formulations, etc. (for the plot see [3])
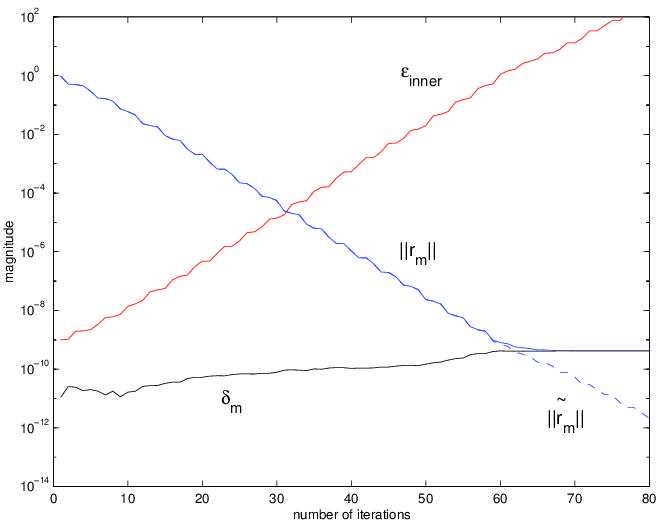 Relaxed approximation of matrix computations for efficiency (for the plot see [12]);
Relaxed approximation of matrix computations for efficiency (for the plot see [12]);
Matrix analysis and solution strategies for PDE discretization methods
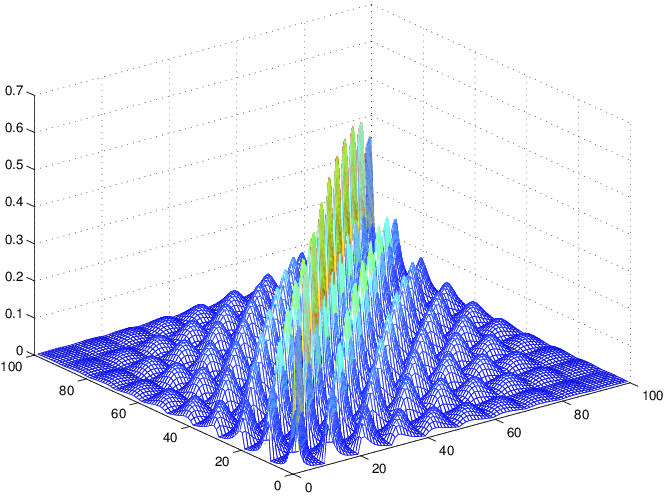
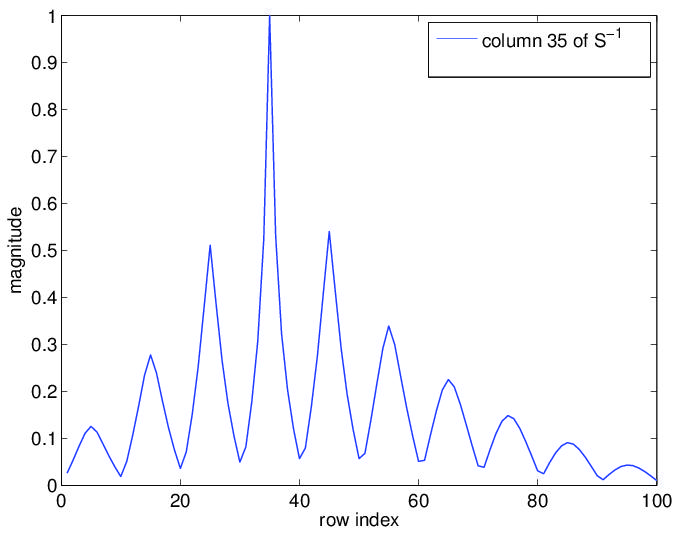 Sparsity pattern analysis and its use in adaptive discretization methodologies
(for the plot see [11]);
Sparsity pattern analysis and its use in adaptive discretization methodologies
(for the plot see [11]);
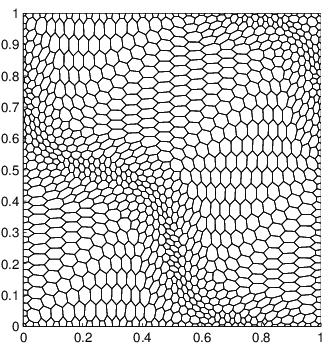
 Definition of key matrices in mimetic FD methods for polygonal/polyhedral meshes (see [13]);
Definition of key matrices in mimetic FD methods for polygonal/polyhedral meshes (see [13]);
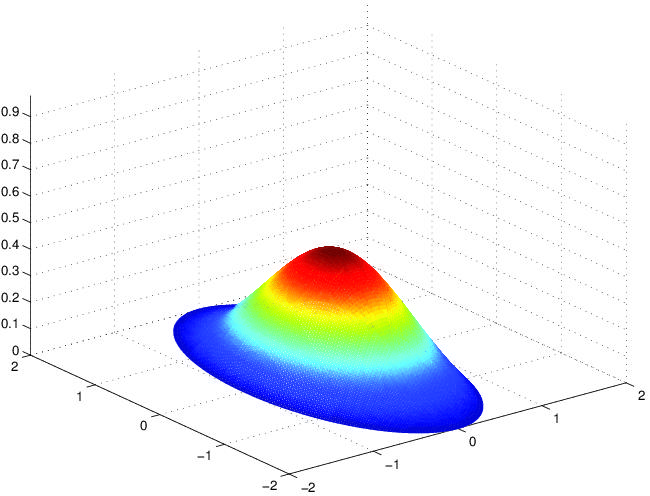
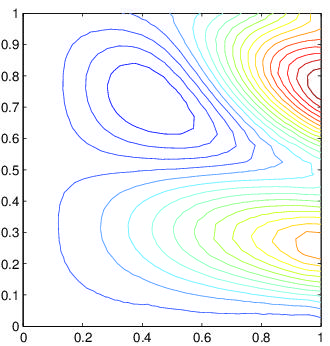
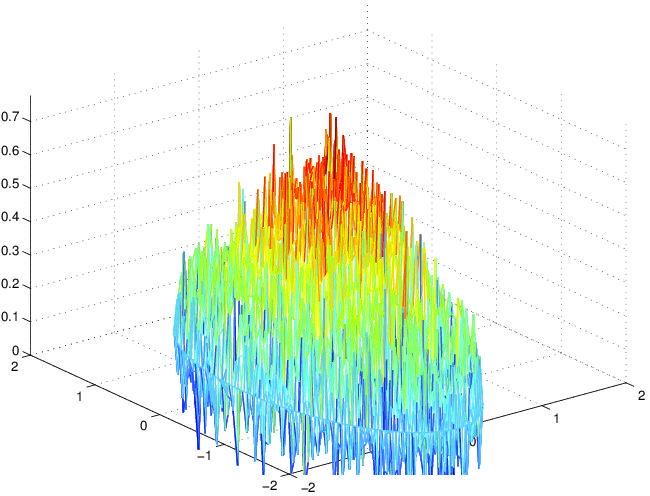 Numerical solution of ill-posed elliptic problems by means of matrix functions
(for the plot see [15]);
Numerical solution of ill-posed elliptic problems by means of matrix functions
(for the plot see [15]);
Numerical treatment of multiparameter and stochastic PDEs for uncertainty quantification
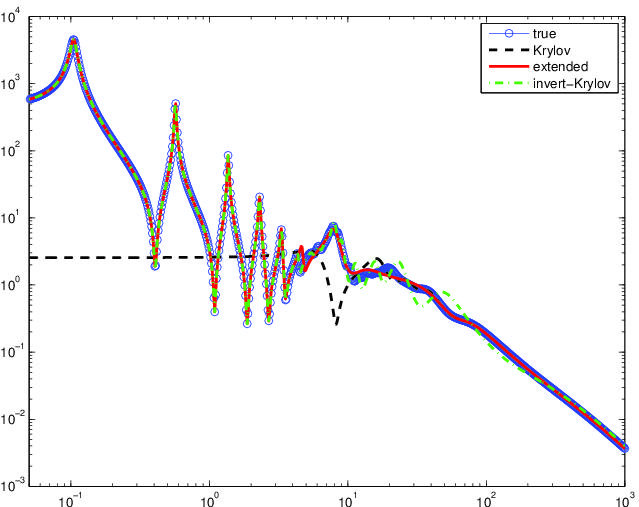 Parameter-dependent problems and Model Order Reduction (for the plot see [4],[7]);
Parameter-dependent problems and Model Order Reduction (for the plot see [4],[7]);
 Parameterized linear equations and stochasticity parameters in
Structure modelling (for the plots see [5])
Parameterized linear equations and stochasticity parameters in
Structure modelling (for the plots see [5])
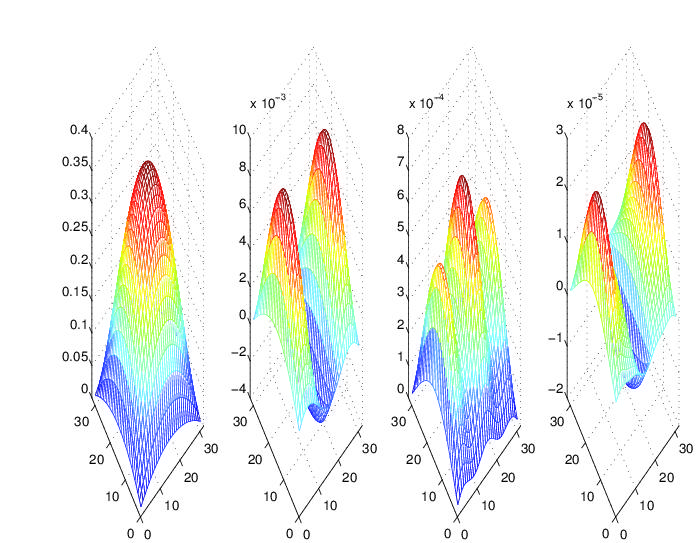 PDEs with random inputs
(for info see [6], data from SIFISS);
PDEs with random inputs
(for info see [6], data from SIFISS);
Numerical modeling of life science phenomena
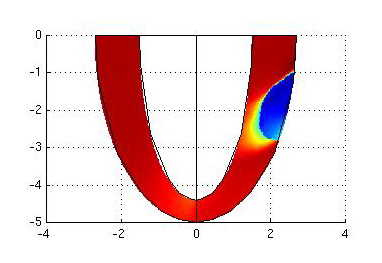
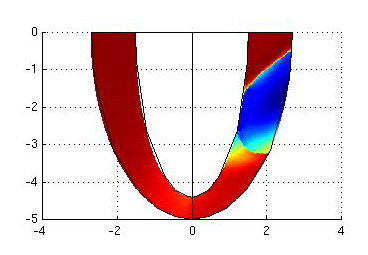 Structured time-dependent systems in Electrocardiology Modelling (for the
plot see [9])
Structured time-dependent systems in Electrocardiology Modelling (for the
plot see [9])
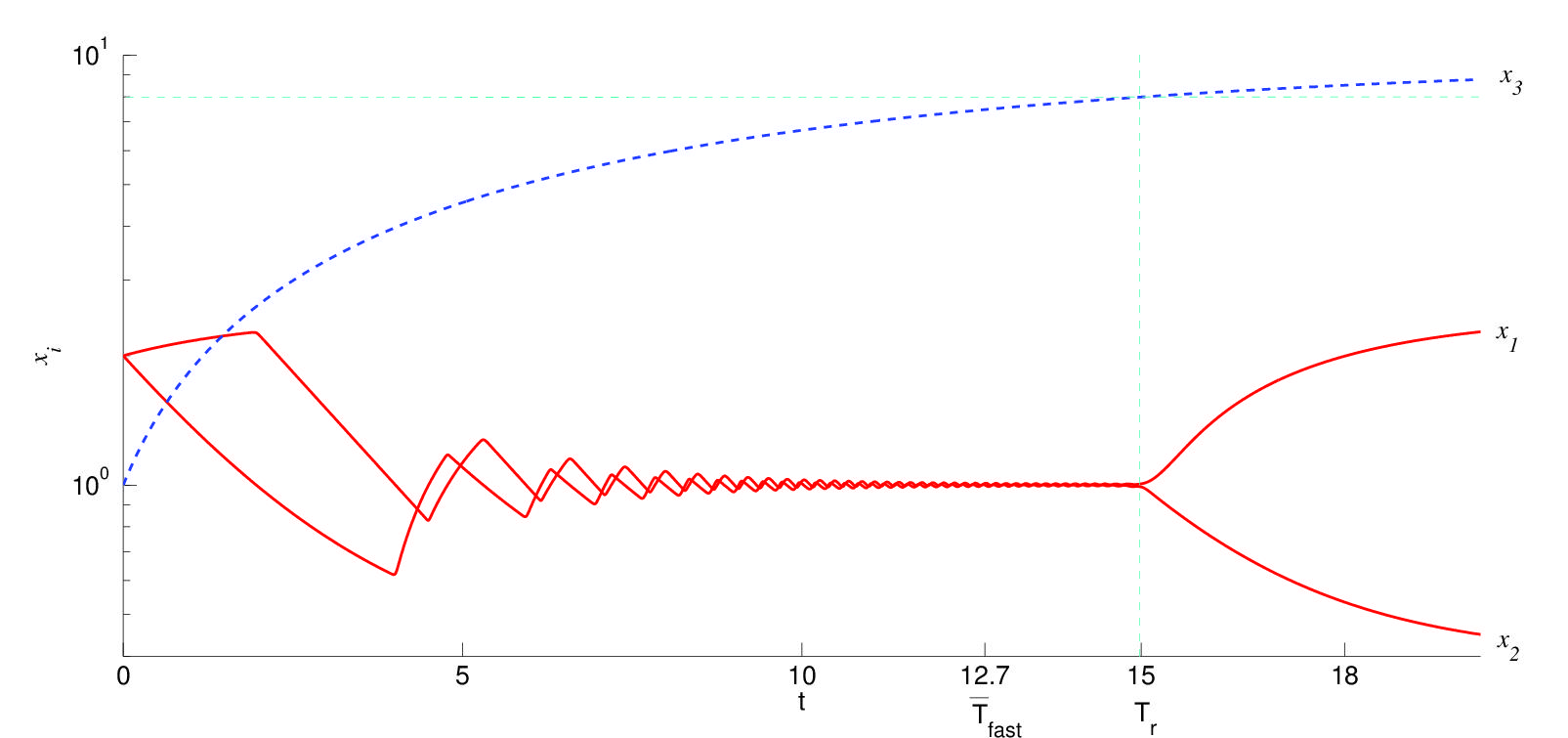 Spectral sensitivity in dynamical systems modelling Gene Networks (for the
plot see [10])
Spectral sensitivity in dynamical systems modelling Gene Networks (for the
plot see [10])
Matrix Analysis and algorithms in Dynamical systems and Control
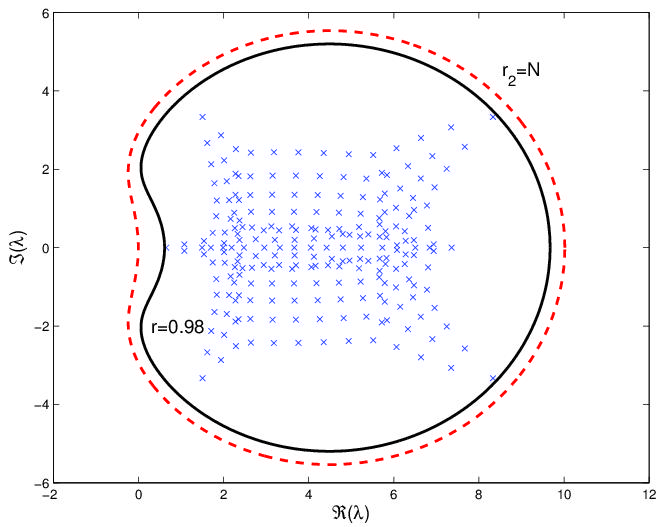
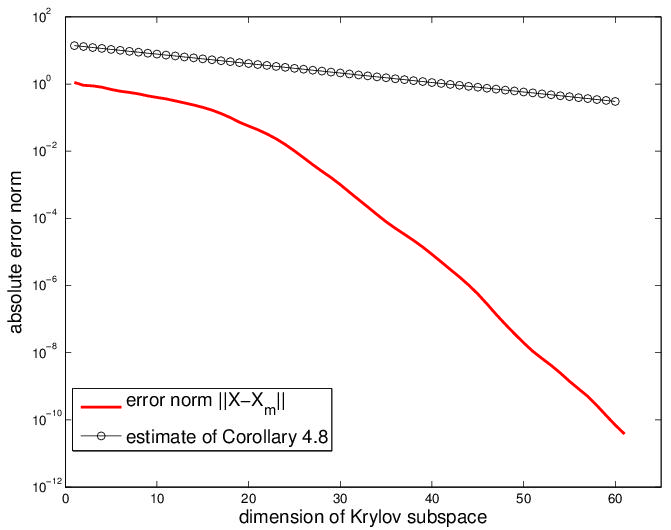 Numerics associated with Lyapunov, Sylvester and Riccati algebraic
equations (for the plot see [14]);
Numerics associated with Lyapunov, Sylvester and Riccati algebraic
equations (for the plot see [14]);
Matrix Computations in Statistics
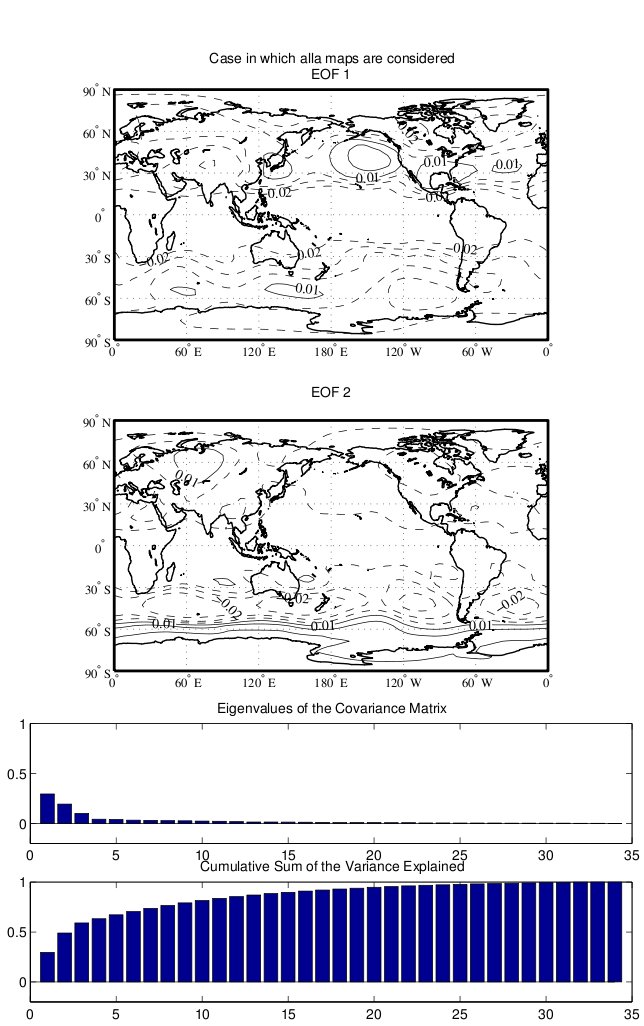 Principal Component Analysis in Athmospheric studies (for the plot see [1])
Principal Component Analysis in Athmospheric studies (for the plot see [1])
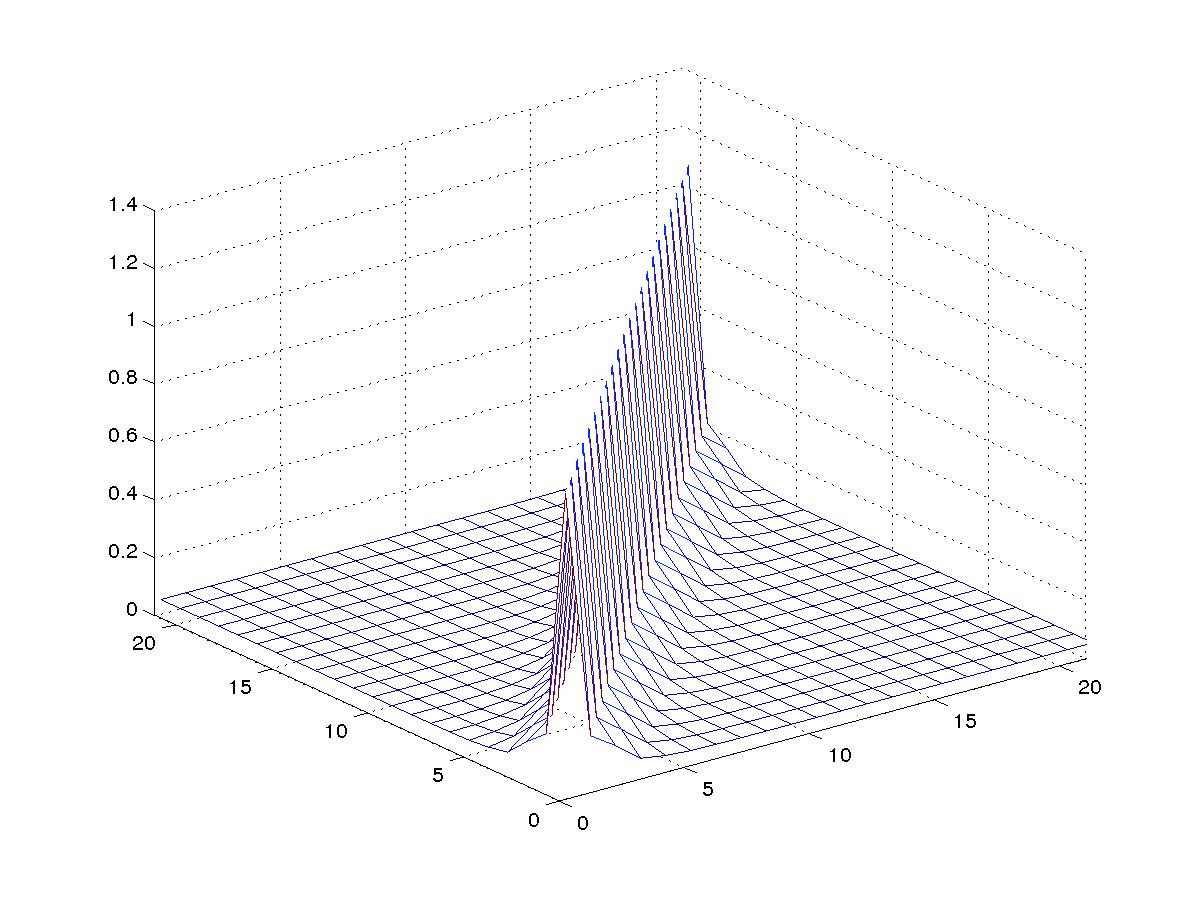 Covariance matrix approximation (for the plot see [2]);
Covariance matrix approximation (for the plot see [2]);
Brief selection of References
(a complete list here ):
- [1]
- A. Navarra and V. Simoncini,A
Guide to Empirical Orthogonal Functions for Climate Data Analysis
2010, 200 p. With online files/update., Hardcover, Springer.
- [2]
- M. Benzi and V. Simoncini,
Decay bounds for functions of matrices with banded or Kronecker structure
SIAM J. Matrix Analysis and Appl. 2015.
- [3]
- I. Perugia and V. Simoncini, Block-diagonal and indefinite symmetric preconditioners for mixed finite element formulations
Numerical Linear Algebra with Appl. v. 7, n.7--8 (2000), pp. 585--616.
- [4]
- V. Simoncini, The Extended Krylov subspace for parameter dependent systems
Applied Num. Math. v.60 n.5 (2010) 550-560.
- [5]
- Gianluca Barbella, Federico Perotti and V. Simoncini
Block Krylov subspace methods for the computation of structural response to turbulent wind
Comput. Meth. Applied Mech. Eng. (CMAME), (2011), v. 200(23-24), pp. 2067-2082. MAME
- [6]
- Catherine E. Powell , David Silvester , and V. Simoncini
An efficient reduced basis solver for stochastic Galerkin matrix equations
MIMS EPrint 2015.64, University of Manchester, UK.
- [7]
- V.Druskin and V. Simoncini,
Adaptive rational Krylov subspaces for large-scale dynamical systems
Systems & Control Letters, 60 (2011), pp. 546-560.
- [8]
- V. Simoncini and F. Perotti,
On the numerical solution of (l2 A + l B + C) x = b and application to structural dynamics
SIAM J. Sci. Comput. v. 23 n.6 (2002) pp. 1876-1898.
- [9]
- M. Pennacchio V. Simoncini, Fast structured AMG Preconditioning for the bidomain model in electrocardiology
SIAM J. Scient. Computing., v. 33, n.2, pp. 721-745 (2011).
- [10]
- Liliana Ironi, Luigi Panzeri , Erik Plahte and V. Simoncini
Dynamics of actively regulated gene networks
Physica D, 240 (2011), pp.779-794.
- [11]
- Claudio Canuto , V. Simoncini and Marco Verani
On the decay of the inverse of matrices that are sum of Kronecker products
Linear Algebra and its Applications, Volume 452, 1 July 2014, Pages 21-39.
- [12]
- V. Simoncini and Daniel B. Szyld ,
Theory of Inexact Krylov Subspace Methods and Applications to Scientific Computing
SIAM J. Scient. Computing, v.25, n.2 (2003), pp. 454-477.
- [13]
- Franco Brezzi , Konstantin Lipnikov and V. Simoncini,
A family of mimetic finite difference methods on polygonal and polyhedral meshes
M3AS: Mathematical Models and Methods in Applied Sciences, v.15 n.10 (2005) pp. 1533-1552.
- [14]
- V. Simoncini and Vladimir Druskin,
Convergence analysis of projection methods for the numerical solution of large Lyapunov equations
SIAM J. Numerical Analysis. Volume 47, Issue 2,pp. 828-843 (2009).
- [15]
- Lars Elde'n and V. Simoncini,
Solving Ill-Posed Cauchy Problems by a Krylov Subspace Method
Inverse Problems, v.25, n.6 (June 2009).



















