Per inoltrare le tue domande mandami un messaggio - con "FAQ" o "domanda" nel Subject - che provvederò ad inserire qui.

Argomenti trattati finora:

Geometria e algebra t

Operazioni binarie interne.
Caratteristica di un anello.
Permutazioni e determinante.
Dimensione e sottospazi somma e intersezione.
Costruzione di rappresentazioni cartesiana e parametrica di sottospazi vettoriali.
Dimensione di sottospazi in forma cartesiana e parametrica.
Passaggio da forma parametrica a cartesiana e viceversa.
Basi e basi ordinate.
Spazio riga, spazio colonna, rango di una matrice.
Matrici di componenti di vettori: in riga o in colonna??
Omomorfismi.
Isomorfismi (1).
Isomorfismi (2), endomorfismi, ecc. 
Nucleo.
Cambiamenti di base.
Significato delle matrici associate alle trasformazioni lineari.
Determinazione di un'applicazione lineare (1).
Determinazione di un'applicazione lineare (2).
Come cambia la matrice di un endomorfismo se cambio base.
Righe, colonne, nucleo, immagine.
Ancora righe e colonne per nucleo, immagine e loro complementi ortogonali.
Trasformazioni di riga e autovalori.
Similitudine e congruenza.
Giacitura.
Interpretazione geometrica dei sistemi lineari.

R. Ehhh, mi tocca di fare un po' di filosofia... La tua difficoltà è, infatti di carattere filosofico: tu ti aspetti delle definizioni e delle argomentazioni semantiche (cioè relative al contenuto, al significato delle cose) mentre tutta la matematica "moderna" (si fa per dire: è così da circa 60 anni) si vuole assolutamente mantenere sul piano sintattico (cioè del puro comportamento, delle regole formali). La differenza è circa quella fra una persona che abbia gusto a giocare a scacchi con dei bei pezzi intagliati artisticamente e uno che sia totalmente indifferente a questo aspetto e si accontenti di pezzettini di carta con scritto "torre", "alfiere" ecc.

Che gusto c'è? Be', se pensi che un calcolatore (almeno per adesso...) può lavorare ESCLUSIVAMENTE in ambito sintattico, capisci quanto sia importante impostare la matematica (e non solo) in questo modo. Anzi, c'è da sorprendersi che quest'impostazione sia fiorita quando ancora i calcolatori elettronici erano pochissimi e primitivi.

(a) Veniamo a noi. La definizione di "operazione" vuol subito mettere in chiaro il suo aspetto sintattico: non gliene frega niente di quale sia (e neanche SE ci sia) un significato per chiamare una certa cosa "operazione"; la definizione pretende solo che tu le presenti una "macchina" (un'applicazione, anche detta funzione) che AD OGNI coppia ordinata di elementi dell'insieme A associ ESATTAMENTE UN elemento di A. A quel punto la chiama "operazione". La teoria prosegue interessandosi alle proprietà formali (associatività, commutatività, esistenza di elemento neutro ecc.) dell'operazione, sempre ignorando volutamente il suo eventuale significato. Perciò viene considerata operazione anche quella che ho definito a lezione (quella che ad ogni coppia di interi (m,n) associa sempre l'intero 42) anche se è completamente idiota, infatti non significa niente e non serve a niente. Anzi, la teoria mette quest'operazione in una luce migliore dalla vecchia e cara sottrazione fra interi, visto che gode della proprietà associativa, mentre la sottrazione (per quanto significativa, utile, importante) no.

(b) Passiamo alla seconda parte della tua domanda. Questa è molto più complicata. Qui si presenta ancora la stessa difficoltà, peggiorata dal fatto che in mezzo ci sarebbe una nozione (relazione di equivalenza e insieme quoziente) che non ho avuto il tempo di definire. Cerco di riassumerla limitatamente all'esempio. Il concetto di "numero razionale" viene introdotto NON per formalizzare l'idea (semantica) di quantità frazionaria (la tipica fetta di torta) ma SOLO per ottenere il vantaggio (sintattico) di costruire un insieme dentro a cui 1) ritrovare gli interi, 2) avere l'inverso moltiplicativo di ogni elemento (diverso da zero). A questo punto le regole del gioco chiedono che costruiamo i nuovi oggetti (che chiameremo appunto "numeri razionali") usando solo ciò che abbiamo fino a quel momento: i numeri interi. Allora utilizziamo coppie ordinate (m,n) con m,n interi ed n diverso da 0 (e qua già puoi riconoscere che m farà da numeratore ed n da denominatore). FERMO! NON pensare a tagliare la tua torta in n pezzi uguali e prenderne m! Questo sarebbe semantico! Ricordati che dobbiamo solo rispettare le due richieste 1) e 2) che ho scritto qui sopra.

Qua devo parlarti di quella maledetta cosa che a lezione ho saltato. Non definisco come numero razionale una sola coppia (m,n) del tipo che ho detto. Insieme ad (m,n) prendo anche tutte le possibili coppie (km,kn) con k intero. anzi, per essere più precisi, insieme ad (m,n) prendo tutte le coppie (p,q) tali che mq=np (il prodotto dei medi sia uguale al prodotto degli estremi). Vedi come siamo stati bravi? Abbiamo sostanzialmente introdotto il concetto di frazioni equivalenti usando semplicemente i numeri interi e la loro operazione di prodotto; nessuna torta tagliata; nessun apporto semantico. Riassumiamo: un numero razionale è dunque un insieme di coppie di interi (di cui il secondo non nullo) fra loro proporzionali. Un esempio di numero razionale, secondo questa costruzione: l'insieme {..., (-4,-6), (-2,-3), (2,3), (4,6), (6,9), ...}. Il numero razionale è tutto l'insieme, ed ogni suo elemento (per esempio (2,3) o (-6,-9)) viene detto suo "rappresentante".

Siamo riusciti a rispettare la richiesta 1)? Sì, basta considerare i numeri razionali che hanno come rappresentanti le coppie (m,1). Questi numeri razionali (dati dalle frazioni in cui il numeratore è multiplo del denominatore, per intenderci) "fanno da" numeri interi.

E la richiesta 2)? Qui bisogna definire le operazioni. La somma, che ti ha messo in difficoltà, è nient'altro che quello che bisogna fare con le frazioni, mettendo a comune denominatore e poi sommando i numeratori. Il prodotto è ancora più semplice: (m,n)*(p,q) è definito come (mp,nq). (In realtà non dovrei parlare della singola coppia (m,n), ma di tutta la sua "classe di proporzionalità"; idem per (p,q)). Cosa succede, allora? Succede che ogni numero razionale (diverso da zero, cioè diverso dalla classe di proporzionalità {...,(0,-2), (0,-1), (0,1), (0,2),...}) ammette inverso. Vuoi vedere? Prendi il numero razionale che sia rappresentato dalla coppia (frazione) (m,n), con m ed n diversi da zero. Allora il numero rappresentato dalla coppia (n,m) è il suo inverso: infatti (m,n)*(n,m) = (mn,nm), che è proporzionale ad (1,1), elemento neutro del prodotto (e corrispondente all'intero 1).

Difficile, eh? Be', come ho detto c'è molta teoria tutta insieme, in questa risposta. Per quello che serve nel corso, concentrati su quello che facciamo sulle matrici, almeno per adesso. Quando tornerai su questa parte alla fine del corso, le cose saranno molto più chiare.

R. Te lo spiego con Z3, insieme (e poi anello, anzi campo) delle classi resto modulo 3. I suoi elementi sono z, u, d.
z è l'insieme di tutti i multipli di 3
u è l'insieme di tutti gli interi che divisi per 3 d nno resto 1
d è l'insieme di tutti gli interi che divisi per 3 d nno resto 2

La somma di due elementi di Z3 è un elemento stesso di Z3.
Esempio: se sommi tutti i multipli di 3 con tutti gli interi a resto 1 riottieni tutti e soli gli interi a resto 1: cioè z+u = u
Se sommi tutti gli interi a resto 1 con tutti gli interi ancora a resto 1 ottieni tutti e soli gli interi a resto 2: cioè u+u = d

Sar - penso - chiaro che z è elemento neutro della somma.

Puoi fare una cosa analoga col prodotto.
Se moltiplichi tutti i multipli di 3 con tutti gli interi a resto 2 ottieni tutti e soli i multipli di 3:
z*d = z.
Idem con gli interi a resto 1:
z*u = z.

Interessante è che c'è un elemento neutro per il prodotto: u. Infatti si può dimostrare che:
se moltiplichi tutti gli interi a resto 1 con tutti gli interi a resto 1 ottieni tutti e soli gli interi a resto 1,
u*u = u
se moltiplichi tutti gli interi a resto 1 con tutti gli interi a resto 2 ottieni tutti e soli gli interi a resto 2,
u*d = d.

Siamo pronti per la caratteristica, che in questo caso è 3. Infatti:
u+u = d,
u+u+u = d+u = z.

R. Una permutazione è un'applicazione biiettiva da un insieme in sé. Per intenderci, è uno dei varii modi per rimescolare l'insieme. Ogni volta che metti in fila i cinque numeri 1, 2, 3, 4, 5 in modi diversi ne stai facendo una permutazione.

Sul libro e sugli appunti troverai tutte le permutazioni dell'insieme {1, 2, 3}, comunque le ripeto qui:

1 2 3    2 3 1    3 1 2    3 2 1    1 3 2    2 1 3

attenzione:
con 1 2 3 intendo l'applicazione che a 1 fa corrispondere 1, che a 2 fa corrispondere 2, che a 3 fa corrispondere 3;
con 2 3 1 intendo l'applicazione che a 1 fa corrispondere 2, che a 2 fa corrispondere 3, che a 3 fa corrispondere 1; e così via.

Non il CALCOLO, ma la DEFINIZIONE di determinante (di una matrice quadrata di ordine n) usa le permutazioni degli indici di colonna. Infatti il determinante è definito come una somma di certi prodotti di elementi della matrice. Quali prodotti? Tutti i possibili prodotti di n elementi, presi in modo che in ogni prodotto sia rappresentata ogni riga e ogni colonna. Per far questo, scriviamo ogni singolo prodotto come

 1        2                n
a     · a  ·   ...   · a
 p(1)   p(2)            p(n)

dove, volta per volta, p(1), p(2), ..., p(n) sono gli indici di colonna permutati secondo la permutazione p.

Siccome gli indici di riga sono 1, 2, ... , n, sei sicuro che tutte le righe sono rappresentate. Ma anche p(1), p(2), ... , p(n) sono tutti i numeri 1, 2, ... , n; infatti p è biiettiva! Quindi in ogni prodotto sono rappresentate tutte le colonne.

Non basta: occorre anche moltiplicare questi prodotti certe volte per -1, certe volte per +1. Quando l'uno e quando l'altro? Dipende dalla permutazione p che hai usato per rimescolare gli indici di colonna: moltiplicherai per (-1)^(numero di coppie in inversione di p), quello che indichiamo con sign(p).
Questo lo devi fare per TUTTE le possibili permutazioni di 1, 2, ... , n e poi devi sommare tutti i prodotti ottenuti. Il numero che ottieni è definito come il determinante della matrice.

Questa è la definizione. Insisto però, come ho già fatto più volte a lezione, che anche se questa definizione è comoda per studiare le proprietà del determinante, non è però la formula più adatta per calcolarlo effettivamente. I teoremi sul determinante consentono di calcolarlo in almeno due modi: portando la matrice in forma triangolare poi moltiplicando gli elementi della diagonale principale, o facendo lo sviluppo di Laplace lungo una riga o una colonna.

Una domanda sorge spontanea: E CHI ME LO FA FARE DI CALCOLARE TUTTI 'STI PRODOTTI ECC. ECC.? Risposta: mi dispiace, ma se vuoi 1) sapere se una matrice è invertibile, 2) sapere se certi vettori sono linearmente dipendenti o indipendenti, hai bisogno proprio del determinante e di nessun altro...

R. Vediamo un po' l'insieme X = {(x,y,z) in R^3 | x=a, y=2·a, z=0, a in R}.
Questo risulta essere un sottospazio vettoriale di R^3, perché è chiuso rispetto alla somma e rispetto al prodotto per scalari. Qual è la sua dimensione?

Bene, cerco una sua base. Mi accorgo che tutti questi vettori sono fra loro proporzionali, e tutti ottenibili come a·(1,2,0). Ma allora l'insieme {(1,2,0)} è un sistema di generatori per il sottospazio X ed anzi, visto che è linearmente indipendente, ne è una base. Contiene un elemento, quindi la dimensione del sottospazio X è uno.

Parliamo di Grassmann.
Mettiamoci, per esempio, nello spazio vettoriale V delle matrici quadrate di ordine 3 su R.

Considera

U = {M in V | M è diagonale}, W = {M in V | M ha elementi tutti nulli fuori dalla diagonale secondaria}

Cioè le matrici di U sono fatte così:

a  0  0
0  b  0
0  0  c

e quelle di W sono così:

0  0  d
0  e  0
f  0  0

Ora, sempre verificando che U e W sono chiusi linearmente si vede che sono sottospazi vettoriali.

Qual è loro dimensione?  Basta trovare delle basi.

Una possibile base per U è quella costituita dalle tre matrici

1  0  0            0  0  0             0  0  0
0  0  0            0  1  0             0  0  0
0  0  0            0  0  0             0  0  1

Una base per W è costituita dalle matrici

0  0  1            0  0  0            0  0  0
0  0  0            0  1  0            0  0  0
0  0  0            0  0  0            1  0  0

Quindi dimU=3, dimW=3.

Qual è l'intersezione? E' costituita dalle matrici che sono sia in U sia in W, quindi le matrici fatte così:

0  0  0
0  g  0
0  0  0

Una base è costituita dalla sola matrice

0  0  0
0  1  0
0  0  0

e la dimensione è 1.

Qual è il sottospazio somma? E' fatto da tutte le matrici somma di una di U più una di W, quindi sono matrici del tipo

a  0  0        0  0  d         a  0  d
0  b  0   +   0  e  0  =     0  h  0
0  0  c         f  0  0          f  0  c

dove h = b+e, ma visto che b ed e sono reali qualunque, anche h è un reale qualunque.

Una base del sottospazio somma è costituita dalle matrici

1  0  0        0  0  1        0  0  0        0  0  0        0  0  0
0  0  0        0  0  0        0  1  0        0  0  0        0  0  0
0  0  0        0  0  0        0  0  0        1  0  0        0  0  1

e la dimensione è 5. Torna tutto:

dimU  +  dimW  =  3 + 3  = 6
dim(UintW)  +  dim(U+W)  =  1 + 5  = 6,

come prevede appunto la relazione di Grassmann.

(Attenzione: per i sottospazi che ho considerato ci sono infinite altre basi possibili; quelle che ho indicato sono solo le più semplici.)

R. Se U è in forma cartesiana, cioè è rappresentato da un sistema di m equazioni lineari omogenee in n incognite, allora la sua dimensione è (n - rango della matrice dei coefficienti). Se è in forma parametrica, cioè le n componenti sono espresse come funzioni omogenee di primo grado di r parametri, allora dimU = (rango della matrice dei coefficienti dei parametri).

Per esempio, se U è il sottospazio di  R^5 rappresentato da

x - y + 3z -u = 0
-x + 2y +z + u + v = 0
x  + y + 11z - u + 2v = 0

allora il rango = 2 della matrice

 1  -1   3   -1   0
-1   2   1    1   1
 1   1  11  -1   2

ci permette di calcolare dimU = 5-2 = 3.

Se W è il sottospazio di R^5 rappresentato da

x =   a - b
y = 5a   - 5c
z =  -a + 2b + c
u =   b + c
v = a + b + 2c

allora il rango = 2 della matrice

 1  -1   0
 5   0   5
-1   2   1
 0   1   1
 1   1   2

ci permette di calcolare dimW = 2.

Attenzione: un errore comune è scambiare le due regole! Un altro errore comune è credere che la dimensione (in forma cartesiana) sia sempre uguale alla differenza n-m; analogo errore è credere che la dimensione (in forma parametrica) sia sempre uguale al numero r dei parametri. Questi due numeri limitano la dimensione, ma possono NON esserle uguali. Infatti puoi avere equazioni cartesiane linearmente dipendenti, ed allora la dimensione sarà maggiore di n-m; analogamente puoi avere colonne dei coefficienti dei parametri linearmente dipendenti, ed allora la dimensione sarà minore di r.

Ma perché valgono le due formule che ho citato all'inizio? Un po' di teoria chiarisce tutto.

Quando rappresentiamo un sottospazio U di V in forma parametrica, lo rappresentiamo come immagine di una trasformazione lineare S avente V come codominio (ed avente come dominio lo spazio dei parametri); S è rappresentata dalla matrice C dei coefficienti. Ma allora sappiamo che la dimensione dell'immagine (cioè di U) è proprio uguale al rango di C.

Se invece rappresentiamo U in forma cartesiana, lo rappresentiamo come nucleo di una trasformazione lineare T avente V come dominio. T è rappresentata dalla matrice A dei coefficienti del sistema. Ma allora l'equazione dimensionale delle trasformazioni lineari ci dice che la dimensione del nucleo (cioè di U) è uguale alla dimensione del dominio (cioè n) meno la dimensione dell'immagine (che è uguale al rango di A).

Ah, già che ci sono: c'è un "bonus". Le colonne della matrice dei coefficienti (in forma parametrica) sono n-ple di componenti di un sistema di generatori per l'immagine, quindi per il sottospazio. Se, studiando il rango della matrice, ne estraiamo un sottoinsieme massimale di colonne linearmente indipendenti, ci siamo procurati una base del sottospazio!

D. 1) Cos'è lo spazio riga e lo spazio colonna di una matrice? 2) la caratteristica (o rango) della matrice?

R. 1) Prendi la seguente matrice A:

  1    3  -1   -1     5    2
-2   -6    2    2   -10   -4
  0    0    0    2     3   -1
 3    9   -3   -5    12    7
-2   -6    2    4   -7   -5
 

Spazio riga:

{ a(1,3,-1,-1,5,2) + b(-2,-6,2,2,-10,-4) + c(0,0,0,2,3,-1) + d(3,9,-3,-5,12,7) + e(-2,-6,2,4,-7,-5) | a,b,c,d,e in R }.

Spazio colonna:

{ f(1,-2,0,3,-2) + g(3,-6,0,9,-6) + h(-1,2,0,-3,2) + j(-1,2,2,-5,4) + k(5,-10,3,12,-7) + m(2,-4,-1,7,-5) | f,g,h,j,k,m in R }.

2) Vediamo cos'è il rango di A. Si può verificare che in effetti tutto lo spazio riga si può esprimere come:

{ a(1,3,-1,-1,5,2) + c(0,0,0,2,3,-1)| a,c in R }.

Infatti la seconda, quarta e quinta riga si possono esprimere come combinazioni lineari della prima e della terza. Dunque l'insieme di generatori dello spazio riga, costituito da tutte le righe, si può ridurre all'insieme della prima e della terza. Queste sono linearmente indipendenti, dunque formano una BASE dello spazio riga. Allora lo spazio riga ha dimensione 2. Questo è il rango (o caratteristica) di A. è dunque il massimo numero di righe linearmente indipendenti presenti nella matrice.

Cosa ci dice il teorema? Che 2 dev'essere anche la dimensione dello spazio colonna. Quindi se trovo due colonne linearmente indipendenti, queste formano una base per lo spazio colonna. Per esempio la prima e la quarta sono linearmente indipendenti. Il teorema dice che la seconda, la terza, la quinta e la sesta colonna sono loro combinazioni lineari. Con quali scalari? Non lo so. Io ho costruito la matrice guardando alle righe, quindi se me lo chiedi SO quali scalari servono per ottenere le varie righe a partire dalla prima e dalla terza riga. Per dare la stessa risposta per le colonne dovrei fare i conti, ma SO che quegli scalari necessariamente ci sono. In definitiva, anche lo spazio colonna si può scrivere in modo più economico a partire dalla base formata da prima e quarta colonna, invece che a partire dall'insieme di generatori formato da tutte le colonne:

{ f(1,-2,0,3,-2) + j(-1,2,2,-5,4) | f,j in R }.

Con questo spero di averti spiegato CHE COSA è il rango. Come calcolarlo è un'altra storia.

D. Quando scrivo la matrice contenente i vettori di una base so che i vettori, secondo le loro componenti, devono essere disposti nella matrice lungo le colonne. Lei però ha svolto un esercizio in cui li disponeva per riga. Perchè? Dov'è la differenza che non riesco a cogliere?

R. Siamo obbligati a mettere le n-ple di componenti in colonna SOLO quando costruiamo la matrice associata ad una trasformazione lineare. E questo dipende da come facciamo il prodotto di matrici.

Negli altri casi, che siano in riga o siano in colonna, l'importante è che ti ricordi come li hai messi. Tanto quello che importa è calcolare il rango. Quando lo fai, il minore di ordine massimo a determinante diverso da 0 è all'incrocio di certe righe e certe colonne della matrice. Bene: quelle righe formano un insieme massimale di righe linearmente indipendenti della matrice; le colonne, idem. A questo punto, se le componenti le hai messe per riga allora puoi subito sapere che i vettori corrispondenti a quelle righe (cioè le righe della matrice grande su cui si trova il minore) formano un insieme massimale di vettori linearmente indipendenti.

(Nota: io preferisco mettere sempre in colonna per non far venire scrupoli come i tuoi. Ma forse è meglio che ti siano venuti!)

R. È effettivamente un concetto molto importante, soprattutto quando l'omomorfismo è biiettivo, cioè un isomorfismo (v. anche le due domande successive a questa, nell'ambito degli spazi vettoriali).
La situazione più generale è quando hai due strutture diverse ma dello stesso tipo: due gruppi, o due anelli, o due spazi vettoriali (in quest'ultimo caso gli omomorfismi vengono chiamati "trasformazioni lineari").
Prendiamo il caso di due gruppi. Per chiarezza prendiamoli diversi (ma si può benissimo avere un omomorfismo di un gruppo in se stesso; v. isomorfismi (2)): (G,*) e (H,@), dove G e H sono insiemi non vuoti e *, @ sono operazioni binarie interne rispettivamente su G ed H. Prima di tutto rispolveriamo la definizione:
un'applicazione f:G->H si dice omomorfismo da (G,*) ad (H,@) se, per ogni g, g' in G accade che

f(g*g') = f(g)@f(g')

cioè prima comporre (con * in G) e poi trasformare ha SEMPRE lo stesso effetto che prima trasformare e poi comporre (con @ in H).

Vediamo questi due esempi, entrambi con (R^3,+) come dominio (+ è la solita somma di terne elemento per elemento) ed (R,+) come codominio (qui + è invece la somma di numeri reali).

F:R^3 -> R
(x,y,z) -> 2x-5y+3z

Perché sia un omomorfismo deve accadere che, comunque io prenda (a,b,c) e (d,e,f) in R^3, valga:

F((a,b,c)+(d,e,f)) = F((a,b,c)) + F((d,e,f))

Vediamo:
F((a,b,c)+(d,e,f)) = F((a+d,b+e,c+f)) = 2(a+d)-5(b+e)+3(c+f) = 2a+2d-5b-5e+3c+3f

F((a,b,c)) = 2a-5b+3f
F((d,e,f)) = 2d-5e+3f

da cui

F((a,b,c)) + F((d,e,f)) = 2a-5b+3f + 2d-5e+3f

ma siccome vale la commutatività della somma di numeri reali, questo numero è proprio uguale a quello visto sopra come F((a,b,c)+(d,e,f)). Perciò F è un omomorfismo dal gruppo (R^3,+) al gruppo (R,+).

Consideriamo ora
G:R^3 -> R
(x,y,z) -> xyz

Anche stavolta voglio sapere se, comunque io prenda (a,b,c) e (d,e,f) in R^3, valga:

G((a,b,c)+(d,e,f)) = G((a,b,c)) + G((d,e,f))

Vediamo:
G((a,b,c)+(d,e,f)) = G((a+d,b+e,c+f)) = (a+d)(b+e)(c+f)

G((a,b,c)) = abc
G((d,e,f)) = def

da cui

G((a,b,c)) + G((d,e,f)) = abc + def

Ora, vedo che i due risultati (a+d)(b+e)(c+f) e abc+def non sono in generale uguali; o almeno non vedo nessuna ragione che lo siano. Ma siamo sicuri che almeno una volta siano diversi?
L'unico modo per accertarcene è escogitare un controesempio. Cerchiamo due terne (a,b,c) e (d,e,f) particolari per cui ci sembra che possano venire risultati diversi. (Consiglio: provare con elementi il più possibile semplici).
Proviamo con (a,b,c)=(1,1,1) e (d,e,f)=(1,1,5). Allora:

G((1,1,1)+(1,1,5)) = G((2,2,6)) = 24
G((1,1,1)) = 1
G((1,1,5)) = 5
G((1,1,1))+G((1,1,5) = 1+5 = 6

Ma 24 è diverso da 6, perciò G NON È un omomorfismo da (R^3,+) ad (R,+).

Segnalo un importantissimo omomorfismo di gruppi, che anzi è (per fortuna) biiettivo, quindi un isomorfismo: il logaritmo (nella base che ti pare, diversa da 1). Con R+ = {reali positivi} e * il solito prodotto di reali,

log:(R+,*) -> (R,+)

è un omomorfismo, in quanto, per ogni x, x' in R+, vale

log(x*x') = log(x)+log(x').

R. La prendo alla larga, come a lezione.

Supponi di avere una mappa molto dettagliata di Bologna, con tutti i vicoletti anche minimi. Allora tu puoi pianificare un percorso semplicemente guardando la mappa. Perché? Per il fatto che l'applicazione (biiettiva) che manda ogni strada della mappa in una strada della città "rispetta la struttura", cioè è fatta in modo che tu vedi via Farini che si immette in via S. Stefano sulla carta, e in effetti v. Farini _vera_ si immette in via S. Stefano _vera_.

Probabilmente in qualche altra città ci sono via Farini e via S. Stefano, ma una non si immette nell'altra (la struttura degli incroci NON è rispettata se passo dalla mappa di Bologna alle strade di quest'altra città).

Quello che abbiamo fra mappa e città è un isomorfismo. Non è un isomorfismo di spazi vettoriali, ma di un altro tipo di oggetto matematico (i grafi; prima o poi li studierai). Quando hai un isomorfismo, uno dei due oggetti in gioco può simulare l'altro. In effetti, la mappa è una simulazione della città.

Se invece avessimo una mappa un po' approssimativa, in cui ci sono solo le vie principali, avresti ancora un applicazione da {strade sulla mappa} a {strade di Bologna}, ma non biiettiva. Quindi potrai pianificare dei percorsi, ma magari non ti accorgerai di certe scorciatoie per certi vicoletti; o ti troverai in una stradina che non ritrovi sulla mappa.

Un po' lo stesso avviene con isomorfismi e trasformazioni lineari fra spazi vettoriali. In particolare gli isomorfismi sono molto più preziosi delle semplici trasformazioni lineari, perché permettono una simulazione completa.

Il più importante isomorfismo è senz'altro quello che, fissata una base ordinata B in V (di dimensione finita n) manda ogni vettore di v nella sua n-pla di componenti rispetto a B. Vuoi sapere se certi polinomi (o certi segmenti, ecc.) sono linearmente indipendenti? Prendine le n-ple di componenti rispetto a B.

stud: "Bene, e adesso che me ne faccio delle n-ple?"

prof: "Be', visto che le n-ple sono linearmente indipendenti se e solo se i polinomi lo sono (per via dell'isomorfismo) basta che io veda se le n-ple sono linearmente indipendenti."

stud: "Sì, ma ho solo spostato il problema: come faccio a sapere se le n-ple sono linearmente indipendenti?"

prof: "AHA! E' qui il bello. Quando il problema si sposta sulle n-ple, basta metterle in matrice e studiare il rango".

stud (sviene per l'emozione).

D. Non ho ben capito il significato di isomorfismo, endomorfismo eccetera.

R. Partiamo dalle definizioni.

Isomorfismo: applicazione lineare biiettiva.
Endomorfismo: applicazione lineare da uno spazio a se stesso.
Automorfismo: endomorfismo biiettivo.

Esempi di isomorfismi (che però non sono endomorfismi):

1) l'applicazione che ad ogni forza applicata nel punto M associa il segmento con un estremo in M, con stessa direzione e stesso verso, con lunghezza in cm uguale all'intensità in Newton.

2) l'applicazione che ad ogni vettore di uno spazio vettoriale V di dimensione n associa la n-pla delle componenti del vettore rispetto ad una base ordinata fissata.

Questi esempi sono particolarmente significativi, perché consentono un'efficace simulazione di uno spazio con un altro. Tuttavia nella definizione rientra anche un esempio non altrettanto interessante come questo:

3) f: R^3 --> {polinomi di gr<3}
   (a,b,c)--> (a-b)+(a+2c)x+(5b-c)x^2

Esempi di endomorfismo.

1) V = spazio dei segmenti con un estremo nel punto fissato M, nello spazio ordinario.
S = un fissato piano passante per M
T = l'applicazione che manda ogni segmento di V nella sua proiezione ortogonale su S.

Commento: siamo in dimensione finita, quindi se voglio dare un esempio di endomorfismo che NON sia un automorfismo, devo farlo NON iniettivo ed automaticamente (per via dell'equazione dimensionale di una trasf. lin.) NON suriettivo.

In dimensione infinita c'è più libertà d'azione:

2) V = C^infinito(R,R). La derivata è un endomorfismo. E' sì suriettivo, ma non è iniettivo, quindi non è un automorfismo.

Esempi di automorfismo.

1) V = solito spazio di segmenti. f = rotazione di un dato angolo attorno ad un dato asse.

2) f: R^2 --> R^2
     (x,y)-->(x-3y, 2x+y)

Questa f è lineare (le funzioni x-3y e 2x+y sono omogenee di primo grado) ed è biiettiva, come si può rilevare dall'invertibilità della matrice

1  -3
2   1

(basta vedere che il determinante è diverso da zero).

R. Credo che la cosa migliore sia considerare degli esempi, visto che la definizione tutto sommato è semplice (è l'insieme dei vettori di V che una trasformazione lineare T da V a W manda nel vettore nullo di W).

T= proiezione
T: R^3-->R^2
(x,y,z)-->(x,y)

Chi va in (0,0)? Tutte e sole le terne (0,0,a) con a in R. Questo è il nucleo di T.

Analogo geometrico:
T: {segmenti con un estremo in N}--> {segmenti con un estremo in N}
       segmento v   --> proiezione ortogonale di v sul piano orizzontale che passa per N

Chi va nel segmento nullo? Tutti e soli i segmenti con un estremo in N, che stanno sulla retta verticale passante per N. Questo è il nucleo.

Invece:
T: {segmenti con un estremo in N}--> {segmenti con un estremo in N}
       segmento v   --> segmento ottenuto ruotando v di 20 gradi attorno alla retta verticale passante per N

Chi va nel segmento nullo? Solo il segmento nullo stesso. Quindi il nucleo è il sottospazio banale; infatti T in questo caso è iniettiva.

T: {funzioni con derivate di ogni ordine}--> {funzioni con derivate di ogni ordine}
        f   --> f' (cioè la derivata di f)

Chi va nella funzione costante nulla? Tutte le funzioni costanti; queste costituiscono il nucleo.

Variante:

T: {funzioni con derivate di ogni ordine}--> {funzioni con derivate di ogni ordine}
        f   --> f" (cioè la derivata seconda di f)

Chi va nella funzione costante nulla? Questa volta il nucleo è costituito dalle funzioni polinomiali a+bx.

D. C'è un esercizio che ci ha proposto su cui ho trovato delle difficoltà. Potrebbe risolverlo indicando bene tutti i passaggi per favore? Ecco l'esercizio:
In uno spazio vettoriale V su R di dim=r, siano B,B1 due basi. In particolare B1=(w1,w2) con w1 rispetto a B (1,5) w2 rispetto a B (2,3);
siano poi v rispetto a B (8,-3) e U il sottospazio vettoriale di V che ha rispetto a B equazione: x-4y=0.
TROVARE LE COMPONENTI DI v RISPETTO A B1 E L'EQUAZIONE DI U RISPETTO A B1.

R. Se metto in colonna (qua è importante: è un cambiamento di base, quindi una trasformazione lineare) le componenti dei vettori di B1 rispetto a B, ottengo la matrice F del cambiamento di base DA B1 A B (attenzione!). Cos'è questa matrice? è quella tale che, se le moltiplico a destra le componenti (x',y') di un vettore v rispetto a B1, saltano fuori le componenti (x,y) dello stesso vettore rispetto a B.

Quindi F=
1 2
5 3

Già, PECCATO CHE A NOI SERVA QUELL'ALTRA. Quale altra? Quella (chiamiamola E) che, se le moltiplichi a destra le componenti rispetto a B, ti dà le componenti rispetto a B1. Però c'è una furbizia: siccome i due cambiamenti di base (da B a B1 e da B1 a B) sono trasformazioni una inversa dell'altra, anche le matrici sono una inversa dell'altra, quindi per trovare E basta fare E=F^(-1).

Cioè E=(-1/7)·
3 -2
-5 1

Adesso, le componenti che t'interessano (cioè le componenti di v rispetto a B1) sono

         8       -30/7
E ·          =
        -3       43/7

OK fin qua? Ora parliamo del sottospazio. Per ottenere l'equazione dello stesso sottospazio, ma rispetto alla base B1, ho bisogno di conoscere x,y in funzione di x', y'. Ma siamo fortunati, perché questo è proprio ciò che ci fornisce la nostra vecchia matrice F:

x            x'
    = F ·
y            y'

cioè
x = x'+ 2 y'
y = 5 x'+ 3 y'

Ora basta sostituire nell'equazione x-4y=0 e ottieni
(x'+2y')-4(5x'+3y')=0
cioè
-19 x' - 10 y' = 0.

R. Semplice: ti riassume in una matrice tutto quello che fa la trasformazione lineare.

Cioè: che T sia una rotazione, una derivazione, un limite, un integrale, una proiezione o chissà cos'altro ancora (v. gli esempi che ho dato parlando di isomorfismi ecc.), purché lineare e fra spazi vettoriali di dimensione finita, tu la puoi simulare con una matrice.

Per usarla devi prendere il vettore v da trasformare (in V), ne leggi le componenti (x1,...,xn) rispetto alla base ordinata (B) fissata nel dominio V, le metti in colonna a destra della matrice, moltiplichi e vengono fuori, sempre in colonna, le componenti (y1,...,ym), rispetto alla base ordinata di arrivo (B', in W) del vettore trasformato T(v):

(y)=A.(x)

R. Innanzi tutto ricordiamo che la matrice è associata ad una trasformazione lineare
fra spazi di dimensione finita
T: V --> W
rispetto ad una base ordinata B=(v1,...,vn) di V e ad una base ordinata B' di W.
La "ricetta" da ricordare per bene è: trasforma il primo elemento v1 della base B
del dominio, scomponi il trasformato T(v1) rispetto alla base B' del codominio, metti in
colonna le componenti, poi lo stesso per il secondo vettore v2, ecc.; la matrice di cui
stai scrivendo le colonne è quella cercata.

Se il dato della trasformazione lineare è proprio la definizione, in termini di
componenti, allora la ricetta generale vale sempre, ma c'è
appunto una scorciatoia: gli elementi della matrice si possono leggere
direttamente dalla definizione; per esempio,se la trasformazione è

T: R^3 --> R^2
(x,y,z)-->(2x+3y+4z, 5x+6y+7z)

allora la matrice che la rappresenta rispetto alle basi naturali è

2  3  4
5  6  7

come puoi verificare applicando la costruzione generale alla base naturale di
R^3.

R. Si tratta di una variante del problema precedente, giustificata dal Teorema fondamentale
delle trasformazioni lineari, che garantisce l'esistenza e unicità di una trasformazione lineare,
quando siano assegnati i trasformati dei vettori di una base del dominio. Poni:

X=
1  2  4
0  1  2
8 -1 -1
 

Y=
1  0 -1
1  2  0

Allora X è invertibile (ha determinante diverso da 0, se no v1, v2, v3 non costituirebbero una base). La matrice cercata A è allora

A= Y X^(-1)

(occhio all'ordine!).

Ragione: A per la prima colonna di X deve dare la prima colonna di Y e così via; allora

A X = Y

adesso moltiplico ambo i membri (a destra) per X^(-1) ed ottengo il risultato.

C'è un ragionamento più sofisticato, che tira in ballo i cambiamenti di base, che porta alla stessa soluzione.  Eccolo.

Se consideri la sola matrice Y, questa è già una matrice che rappresenta l'applicazione T, solo che la rappresenta rispetto alla base B1=(v1,v2,v3) in R^3 e alla base canonica C2 in R^2. Cioè: se moltiplico Y per la terna (in colonna) di componenti di un vettore v rispetto a B1, esce la coppia delle componenti del vettore trasformato T(v) rispetto alla base naturale (cioè T(v) stesso, visto che qui stiamo usando la base canonica). Già, ma noi vogliamo far entrare le componenti rispetto alla base canonica C3 di R^3, non quelle rispetto a B1. Bene, allora mettiamo a destra di Y una specie di "adattatore" (v. la mia metafora nella risposta su endomorfismi e cambiamenti di base), cioè la matrice P del cambiamento di base da C3 a B1; a questo punto la matrice prodotto Y P accoglie in ingresso le componenti di v rispetto a C3 e (passando per le componenti rispetto a B1, ma chi se ne frega?) butta fuori le componenti di T(v) rispetto a C2. Proprio quello che volevamo! Quindi la matrice richiesta A è proprio Y P.

Ma chi è P? Be', che vogliamo o no, una matrice di cambiamento di base ce l'abbiamo già: è X. Solo che X è la matrice del cambiamento da B1 a C3, cioè l'inverso di quello che vogliamo noi. Ma per fortuna l'applicazione endomorfismi --> matrici è un isomorfismo di anelli, quindi per fare il cambiamento di base inverso (quello che serve a noi) basta invertire la matrice. Dunque P = X^(-1) e A = Y X^(-1).

D. Non capisco la risoluzione di un esercizio trovato su un libro. Dà una base B=(a,b,c) e una base B1=(a1,b1,c1), dà le componenti dei vettori della base B rispetto a B1 (a=a1-3b1...) e chiede: determinare la matrice A1 che rappresenta, rispetto alla base B1, l'endomorfismo T su V avente, rispetto a B, la matrice A=...... come matrice associata.
Soluzione: "sia M la matrice del cambiamento di base da B a B1. Vale A1=M.A.M' (dove M' è l'inversa di M)".
Domanda: perché??? Io avevo fatto così: ho calcolato la matrice M del cambiamento di base, poi ho direttamente moltiplicato M per A. Non capisco l'introduzione dell'inversa della matrice del cambiamento di base. Comunque sia, che cosa ottengo con il mio calcolo?

R. Ecco la mia metafora preferita.

Ho comperato un "invertitore di fase". Non chiedermi a cosa serva; diciamo che ne avevo bisogno. Entra la corrente alternata (che ha una certa "fase", fìdati) ed esce con la fase invertita. [Immaginalo, per favore, lì davanti a te con il filo e la spina d'ingresso a destra (capirai dopo perché) e la presa d'uscita a sinistra.]

Solo che c'è un problema: è tedesco. Quindi sia l'ingresso (una spina "maschio") sia l'uscita (una presa "femmina") sono di quelle tonde, speciali, appunto tedesche.

Come facciamo a mettere insieme un invertitore di fase italiano?

Ecco: aggiungiamo DUE adattatori. Uno con maschio italiano e femmina tedesca, per la corrente in ingresso, ed uno con maschio tedesco e femmina italiana per l'uscita. Voilà!

Veniamo a noi. Abbiamo una matrice A che accetta in entrata le componenti di v e dà in uscita le componenti di T(v). Sia in entrata sia in uscita le componenti sono scritte rispetto a B.

Io invece voglio usare (sia in ingresso sia in uscita) le componenti rispetto a B1. Come facciamo a mettere insieme la matrice giusta?

Ecco: aggiungiamo DUE cambiamenti di base. Uno che accetta componenti rispetto a B1 e restituisce componenti rispetto a B per il vettore v in ingresso, ed uno che accetta componenti rispetto a B e restituisce componenti rispetto a B1 per il vettore T(v) in uscita. Voilà!

Ehi, attenta: ricordati che il vettore v (voglio dire: la sua n-pla di componenti) "entra" da destra, quindi è a destra che ci vuole la matrice M', che è quella del cambiamento di base da B1 a B. Nota che M' è in realtà proprio la matrice che ottieni subito senza alcun calcolo, mettendo in colonna le componenti dei vettori di B1 rispetto a B. M invece la calcoli invertendo M'; M va poi moltiplicata a sinistra, per trasformare (da B a B1) le componenti di T(v). Perciò A1 = M.A.M'.

Ah, la tua ultima domanda. A questo punto avrai già intuito la risposta: il solo prodotto M.A fornisce sì le componenti di T(v) rispetto a B1, PERÒ accetta in ingresso le componenti di v rispetto a B. (V. l'ultima parte della mia risposta alla seconda domanda sul reperimento della matrice associata ad una trasformazione lineare).

Posso parlare di un sottospazio vettoriale anche in assenza di una qualsiasi trasformazione lineare. Tuttavia è vero che, quando rappresento un sottospazio (di uno spazio vettoriale V) in forma cartesiana, è come se mi inventassi una trasformazione lineare (che parte da V) su misura per lui, di cui esso è il nucleo.

È altrettanto vero che, quando lo rappresento in forma parametrica, è come se mi inventassi una trasformazione lineare (che arriva in V, diversa da quella di prima) di cui esso è l'immagine.

Detto questo, partiamo invece da una matrice che rappresenti una trasformazione lineare. Allora valgono le seguenti cose (v. anche la domanda precedente).

1) Le colonne sono generatori (non necessariamente linearmente indipendenti) dell'immagine (meglio: sono le m-ple di componenti di generatori dell'immagine).

2) Le righe sono n-ple di coefficienti di equazioni cartesiane (non necessariamente linearmente indipendenti) del nucleo.

A questo punto valgono anche:

3) Le colonne sono m-ple di coefficienti di equazioni cartesiane (non necessariamente linearmente indipendenti) del complemento ortogonale dell'immagine.

4) Le righe sono generatori (non necessariamente linearmente indipendenti) del complemento ortogonale del nucleo (meglio: n-ple di componenti di suoi generatori).

R. 1) Similitudine e congruenza si assomigliano sia come definizione sia come "utilità".

Definizioni (A e B matrici quadrate di ordine n su K):

A si dice simile a B se esiste una matrice P in Gln(K) tale che B=P^(-1) A P.

(A e B simmetriche) A si dice congruente a B se esiste P in Gln(K) tale che B=Pt A P

Utilità (teoremi):

A e B risultano simili se e solo se rappresentano uno stesso endomorfismo rispetto a basi B1 e B2.

A e B risultano congruenti se e solo se rappresentano una stessa forma quadratica rispetto a basi B1 e B2.

2) Un algoritmo generale per verificare la similitudine c'è, ma NON nell'ambito del nostro corso.

Per quanto compreso nel nostro programma, la situazione, date due matrici A e B quadrate dello stesso ordine su K, è la seguente.

Se A e B sono entrambe diagonalizzabili per similitudine (il che non è poca roba, visto che ci cascano dentro tutte le reali simmetriche) allora sono simili se e solo se hanno polinomi caratteristici identici.

Se A è diagonalizzabile per similitudine ma B no, allora non sono simili.

Se né A né B è diagonalizzabile per similitudine, allora NON abbiamo risposta se i polinomi caratteristici sono identici. Abbiamo risposta negativa se differiscono anche solo per un coefficiente. (In realtà potremmo sapere già qualcosa anche con i polinomi identici; se la molteplicità geometrica di un autovalore è diversa per A e per B, allora le due matrici non sono simili).

3) Tutto è molto più semplice per la congruenza: due matrici simmetriche dello stesso ordine, su C, sono congruenti se e solo se hanno lo stesso rango; due matrici simmetriche dello stesso ordine, su R, sono congruenti se e solo se hanno la stessa somma delle molteplicità degli autovalori positivi e la stessa somma delle molteplicità degli autovalori negativi.

D. Potrebbe illustrarmi delle motivazioni per lo studio degli spazi proiettivi, e magari un modo per immaginarmeli?

R. (piuttosto lunga)   :-(   Mettetevi comodi...

MOTIVAZIONI

1) (tecnica vettoriale)
Vorremmo usare le tecniche vettoriali e matriciali in modo più diretto che non negli spazi affini. In particolare vorremmo usare le coordinate direttamente come componenti, i punti direttamente come vettori; vorremmo poter trattare la dipendenza di punti esattamente come la lineare dipendenza di vettori.

2) (visione artificiale e grafica al calcolatore)
La necessità di tener conto della distorsione prospettica fa sì che si debbano effettuare trasformazioni più "libere" delle trasformazioni affini, ma che mandino ancora rette in rette; in particolare, la libertà che si richiede è quella di trasformare rette parallele in rette incidenti. Ciò impone di introdurre le direzioni come nuovi "punti".

3) (robotica meccanica)
Spesso si devono usare trasformazioni affini, ma la parte traslazionale (la colonna da sommare dopo aver fatto il prodotto) è scomoda; si preferisce usare una dimensione "ausiliaria" in più, ma dover fare solo prodotti di matrici.

4) (meccanica quantistica)
gli "stati" della meccanica quantistica sono proprio classi di proporzionalità di funzioni non nulle.

5) (geometria affine)
Dà fastidio che certi insiemi che hanno manifestamente k gradi di libertà siano invece descritti da k+1 parametri. Esempi tipici: fascio di rette per un punto in un piano, fascio di piani per una retta nello spazio (k=1), stella di rette per un punto nello spazio (k=2). Il fatto che i gradi di libertà siano k dipende dalla constatazione che ogni "oggetto" non è in realtà rappresentato da una sola (k+1)-pla (non nulla): (k+1)-ple proporzionali rappresentano lo stesso oggetto. Per accorgercene, possiamo passare ai rapporti di k di tali parametri rispetto al parametro restante. (Questo è poi il succo delle "carte affini"). Però se fai così escludi alcuni oggetti. Tipico esempio: se invece dei numeri direttori l,m di una retta (x/l = y/m o meglio mx=ly) usi il coefficiente angolare h=m/l (rappresentando la retta come y=hx) ti rendi meglio conto che si ha un solo grado di libertà, ma a prezzo di escludere dalla rappresentazione la retta x=0. Con la stella di punti nello spazio è anche peggio: perdi infinite rette.

DEFINIZIONE FORMALE

Uno spazio proiettivo è una terna (V, P, f), dove V è uno spazio vettoriale, P un insieme (detto insieme dei punti), t:V-{nullo}->P un'applicazione tale che f(v)=f(v') sse v' è proporzionale a v. Si definisce, come dimensione dello spazio proiettivo, quella dello spazio vettoriale -1 (calma! si vedrà dopo perché).

ESEMPI

1) (sp. proiettivo associato ad uno spazio vettoriale)
P={classi di proporzionalità di vettori non nulli di V} f(v)=[v] (la sua classe di proporzionalità). Immagino, per esempio, V come lo spazio vettoriale dei segmenti uscenti da un fissato punto M di questo spazio geometrico. Ogni "punto" è in realtà una retta vettoriale (una specie di spaghetto) privata del vettore nullo. Siccome dimV=3, si dichiara che dimP=2. Un piano proiettivo è dunque una specie di "truciolone".

2) (ampliamento proiettivo di uno spazio affine)
Prendi uno spazio affine A di dim=n. (Nota: n. Ecco perché c'è quella differenza di dimensioni). Fissaci sopra un riferimento affine. V=K^(n+1); P=unione di A e dell'insieme delle sue direzioni (classi di proporzionalità di vettori liberi). La definizione di f è spezzata in due parti: a certe classi di (n+1)-ple si associano punti, ad altre direzioni.

                                      Q di coord. (X1/Xo,...,Xn/Xo)    se Xo diverso da 0
f([(Xo, X1,...,Xn)])= {
                                      classe di proporz. del vettore libero
                                      di componenti (X1,...,Xn)    se Xo=0

COMMENTI

Il primo esempio sembra dire poco, perché pare antiintuitivo, poco geometrico. C'è da dire che, invece, è una situazione abbastanza naturale: quando vediamo un punto, in realtà ciò significa che un fotone arriva da quel punto al nostro occhio; se vediamo tre punti allineati, vuol dire che le tre rette percorse dai tre fotoni stanno in uno stesso piano passante per il nostro occhio. In realtà è lo spazio affine (e quello euclideo) che è un'astrazione. Ma noi ci siamo tanto abituati a quest'astrazione, che ci pare più naturale della natura (che, invece, è più proiettiva, come spero di averti mostrato).

Anche il cinema assomiglia a questa situazione: ogni punto sullo schermo corrisponde in realtà ad una retta uscente dal proiettore; ogni retta corrisponde ad un piano uscente dal proiettore. Due rette incidenti sono proiettate da due piani (uscenti dal proiettore) che si intersecano in una retta (anche lei uscente dal proiettore). Cosa succede a due rette parallele? Anche loro sono proiettate da due piani uscenti dal proiettore; se questo proiettasse a 360 gradi, e non solo l'angolo solido che colpisce lo schermo, vedremmo che anche questi due piani si intersecano in una retta; è però una retta che necessariamente NON interseca il piano dello schermo. Questa retta vettoriale (sostanzialmente uguale a quella di prima, che proiettava il punto d'incidenza) non corrisponde più ad un punto del piano dello schermo, ma ad una sua direzione. Abbiamo vinto! Oggetti comparabili (rette vettoriali, o vettori loro rappresentanti) rappresentano talvolta punti, talvolta direzioni; e basta un tranquillo endomorfismo (per esempio ruotare un pochino il proiettore) per trasformare rette-che-rappresentano-punti (dette "punti propri") in rette-che-rappresentano-direzioni ("punti impropri") e viceversa. Forte, no?

Ma questo è anche il succo del secondo esempio. Solo che ad un punto o ad una direzione non associ una retta geometrica, come ho fatto qua sopra, ma direttamente un oggetto spendibile nella teoria delle matrici: una (n+1)-pla di numeri.

D. Può indicarmi un libro che spieghi come visualizzare su uno schermo di pc grafica 3d con gli spazi proiettivi?

R. Sì; c'è il

Penna M.A., Patterson R.R., "Projective geometry and its application to computer graphics", Prentice-Hall, 1986.

D. In uno spazio euclideo E^4 , rispetto ad un riferimento cartesiano, si considerino le rette r ed s di equazioni cartesiane, rispettivamente,

  |y=0           |x=y
  |z=-1          |z=y+12
  |z+t-1=0    |x-y+t=5

a) Si calcoli la distanza fra r ed s.
b) Si trovi un sistema lineare che rappresenti lo spazio che le congiunge.

R. Allora, prima di tutto date comunque due rette in uno spazio E^n, c'è uno spazio di dimensione minima che le contiene (il "congiungente"); se loro sono parallele o incidenti, sarà un piano; altrimenti sarà un sottospazio 3-dimensionale. Ma su questo torno dopo.

Comunque, l'esistenza di questo spazio mi garantisce che i metodi soliti per la distanza fra due rette andranno bene (con opportuni adattamenti).

a) Propongo questo:

prendi il generico punto R_u su r ed il generico punto S_v su s. Congiungili con una retta; il segmento R_u S_v di minima lunghezza (quello che realizza la distanza fra le due rette) è ortogonale ad entrambe r ed s.

Risolvendo i sistemi, mettiamo in forma parametrica:
x=u, y=0, z=-1, t=2;       x=v, y=v, z=v+12, t=5,
da cui
R_u=(u,0,-1,2),      S_v=(v,v,v+12,5).

Ora, della retta R_u S_v ci servono solo i numeri direttori, che otteniamo come differenza di coordinate:

(h,l,m,n) ~ (v-u, v, v+13, 3).

Condizioni di ortogonalità con r e con s: si vede dalle forme parametriche che numeri direttori per le due rette sono rispettivamente

(1,0,0,0), (1,1,1,0).

Le condizioni diventano allora:

1·h + 0·l + 0·m + 0·n = 0,       1·h + 1·l + 1·m + 0·n = 0,

cioè

h = 0,    h + l + m = 0,

da cui (usando ora i parametri u e v)

v-u = 0,       v-u + v + v+13 =0,

dunque (risolvendo)

u = v = -13/2

Sostituisci questi valori in R_u ed S_v ed ottieni gli estremi del segmento di minima lunghezza:

R=(-13/2,0,-1,2),       S=(-13/2,-13/2,11/2,5).

Calcola la distanza euclidea, ed ottieni radice di 187/2.

b) Sottospazio congiungente: lo ottieni da due punti di r e due punti di s.

I punti si ottengono fissando due valori (per es. 0 e 1) per i due parametri u e v:

A=(0,0,-1,2),   B=(1,0,-1,2),      C=(0,0,12,5),    D=(1,1,13,5).
Subito servono i vettori liberi AB, AC, AD (dalle differenze di coordinate); il sistema si ottiene imponendo al generico vettore libero AP di essere combinazione lineare di questi, cioè imponendo rango 3 (e dunque det=0) alla matrice:

1   0    1    (x-0)
0   0    1    (y-0)
0   13   14   (z+1)
0   3    3    (t-2)

da cui l'equazione - 3y + 3z - 13t + 29 = 0.

D. 1) Considerando un cono isotropo, in dim V =3, questo è "graficamente" sempre un cono?
2) Sapendo che il vertice (in V) appartiene al cono isotropo, come mai possono esistere delle coniche (in P) (es: circonferenze e ellissi) che non hanno vertice? Infatti, se il cono isotropo fosse proprio un cono (graficamente!!), e considerando la conica come l'immagine I([q]) (e quindi graficamente come il piano intersecato con il cono), ogni conica dovrebbe possedere un vertice, mentre in realtà non è così!
Tutto ciò porta, forse più propriamente, ad un'altra domanda:
3) Che cosa è esattamente il vertice? Come lo posso "vedere graficamente" nel vettoriale e nel proiettivo?

R. 1) No: può essere il solo vettore nullo (es.: x^2+y^2+z^2), o un'unione di due piani (es.: xy), ecc.

2) Se il cono isotropo, di una forma rappresentante la conica, è "davvero" un cono, allora il vertice della forma è dato dal solo vettore nullo, perciò dà luogo ad un vertice (proiettivo) della conica vuoto. Graficamente: guarda la sua intersezione con un piano non passante dal vettore nullo.
Se intersechi il cono isotropo della forma x^2+y^2-z^2 con il piano z=1 trovi proprio una bella circonferenza (vertice vuoto). Se invece intersechi lo stesso piano con il cono isotropo della forma xy trovi due rette; il punto (0,0,1) comune alle due rette è il vertice (proiettivo) corrispondente al vertice (vettoriale)
   x=0
{
   y=0

che è la retta comune ai due piani x=0 ed y=0 la cui unione forma il cono isotropo (vettoriale).

3) Questa volta vince il proiettivo sul vettoriale! Prima guarda se ci sono, nell'immagine, punti doppi (tali, cioè, che ogni retta che passa di lì sia tangente in uno dei due sensi della definizione). I punti doppi formano il vertice (proiettivo) della conica. Ora, se immagine e vertice li vedi su uno schermo del cinema, guarda i raggi che provengono dal proiettore e vedrai cono isotropo (che proietta l'immagine) e vertice (che proietta appunto il vertice).

D. Cos'è la polarità? Come posso immaginarla?

R. Ho l'abitudine di proporre, metaforicamente, una proporzione: una forma quadratica sta alla sua forma bilineare simmetrica associata come l'immagine di una quadrica sta alla sua polarità. Quindi vedo la polarità come "l'altra faccia delle quadriche", rispetto all'immagine, così come forme bilineari e quadratiche sono due facce di una stessa medaglia. Ti propongo due interpretazioni della polarità: una algebrica e una geometrica.

Polarità dal punto di vista algebrico. Immagina una qualunque froma bilineare simmetrica come una generalizzazione dei prodotti scalari (in effetti, questi hanno in più di essere forme definite positive). Userò, ora, il termine "ortogonali", per due vettori v e w, per dire che la fissata forma bilineare simmetrica valga zero sulla coppia (v,w). A questo punto, l'immagine di una quadrica (rappresentata dalla forma quadratica associata alla forma bilineare) è l'insieme dei punti rappresentati dai vettori "ortogonali a se stessi". Ne abbiamo già parlato nella risposta su vertice e cono isotropo. Non deve fare alcuna meraviglia che per l'ortogonalità "vera" solo il vettore nullo sia ortogonale a se stesso: è insito nella definizione di forma definita. Nella generalizzazione che stiamo facendo, invece, ci possono essere vettori non nulli in questa situazione, dunque un'immagine non vuota. E la polarità? Be', qual è l'insieme dei vettori w coniugati ad un fissato v? È l'insieme dei w "ortogonali" a v. (Attenzione: NON pensare a questa "ortogonalità" in senso geometrico!). Questo insieme può anche essere tutto lo spazio vettoriale (vedi nuovamente la nozione di vertice); ancora una volta questo non può accadere se la forma è un vero prodotto scalare. Altrimenti, questo insieme è un iperpiano (dello spazio vettoriale) che dà luogo, dunque, ad un iperpiano dello spazio proiettivo: l'iperpiano polare del punto [v] rispetto alla quadrica.

Polarità dal punto di vista geometrico. C'è un caso in cui la polarità ha un senso abbastanza immediato: quando il polo appartiene all'immagine (ma non al vertice). In tal caso l'iperpiano polare è l'iperpiano tangente alla quadrica nel punto. (Attenzione: quello di iperpiano tangente è un concetto NON banale; vedi la nota nel Chicken's Corner). Unendo questo fatto alla legge di reciprocità, otteniamo un'intepretazione interessante per gran parte dei punti dello spazio: quelli come il punto P nella figura qua sotto, relativa ad una conica del piano. Immaginiamo di porre in P una lampadina; una parte dell'immagine della conica sarà illuminata, un'altra al buio. La transizione avviene nei punti A e B, per i quali la tangente passa proprio per P. Dunque P è il polo della retta AB, per la legge di reciprocità. Analogamente, nello spazio, se mettiamo una sorgente luminosa in un punto P "esterno" alla quadrica, la parte illuminata della quadrica è separata da quella al buio da una conica, che si ottiene intersecando la quadrica stessa con il piano polare di P. (N.B.: "punto esterno" è un concetto che qui uso in senso intuitivo, ma che è definito proprio come un punto il cui iperpiano polare ha intersezione reale e non degenere con l'immagine).

Consiglio di giocare con il programma Polar, scritto (da una ragazza affascinante) apposta per far imparare meglio la polarità.

D. Cosa sono praticamente i diametri e gli iperpiani diametrali?

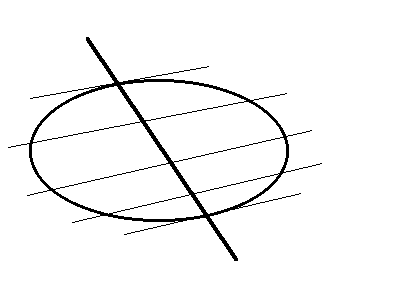
R. (Vedi anche la nota nel Chicken's Corner). Riprendiamo l'interpretazione fisica della risposta alla domanda sulla polarità; già, se immaginiamo di allontanare il punto luminoso dalla quadrica, lungo una fissata direzione, vediamo che la curva di confine fra luce ed ombra "tende" ad una certa curva. Ma non c'è bisogno del pesante concetto di limite. Pensiamo di illuminare la quadrica, invece che con una lampadina, con un grosso riflettore che spara fotoni lungo la direzione rappresentata dal punto improprio P. Anche questa volta c'è una conica di confine fra luce e buio, ed è proprio l'intersezione della quadrica con il piano diametrale coniugato alla direzione rappresentata da P. (E' la conica a cui tendevamo prima).

Attenzione alla terminologia: in dimensione due "diametro" significa iperpiano diametrale; nelle dimensioni superiori significa retta intersezione di iperpiani diametrali.

D. Quando si trattano gli iperpiani diametrali, si parla di una certa proprietà di simmetria. Di cosa si tratta?

R. Immagina di essere nella situazione della risposta precedente, e di avere individuato il piano diametrale coniugato alla direzione rappresentata dal punto improprio P. Ora immagina di sparare, lungo questa stessa direzione, proiettili con tanti fucili fra loro paralleli. Per ogni proiettile si verifica che il foro praticato nel piano diametrale è punto medio fra i due fori (se ci sono) praticati nella immagine della quadrica (vedi l'illustrazione qua sotto per un'ellisse ed una parabola). Questa è una proprietà di simmetria della quadrica (o conica, o iperquadrica) molto utile (l'abbiamo usata per il robot mobile SAM); in generale è una simmetria non ortogonale. Diventa simmetria ortogonale quando il piano (o iperpiano) diametrale è ortogonale alla direzione coniugata (cioè quella rappresentata dal suo polo). Questa è una situazione così notevole, che si usa un termine speciale: (iper)piano principale (asse, in dimensione due).

D. Quando fa la domanda "classificazione proiettiva delle coniche (o quadriche, ecc.)" cosa vuole che si risponda?

R. Prendiamo, per esempio, la classificazione proiettiva delle coniche in campo reale. "Classificazione" significa, per me, due cose.

La prima è quella parte di teoria che definisce l'equivalenza proiettiva delle coniche, che la mette in relazione con la congruenza di matrici, e che porta - attraverso la segnatura non ordinata del discriminante - a stabilire quali sono tutte e sole le classi di equivalenza proiettiva di coniche. Questa è la parte che voglio sentir descrivere bene; m'interessa molto meno il dettaglio di come sono fatte le singole coniche.

La seconda accezione è quella di algoritmo che porta da un'equazione data fino alla determinazione della classe di equivalenza cui appartiene la conica con quell'equazione. Posso quindi chiedere in cosa consiste l'algoritmo.

D. Mi potrebbe esporre uno o più metodi per distinguere un cono reale da un cono immaginario e un cilindro reale da uno immaginario?

R. Un metodo sicuro ma un po' lento consiste nel trovare la segnatura: che si tratti di un cono (A00 diverso da zero) o di un cilindro (A00=0), abbiamo {3,0} per quello immaginario, {2,1} per quello reale.

Se però si tratta di un cono c'è una scorciatoia: il minore M00 ti dice tutto. Se è definito (positivo o negativo) il cono è immaginario; infatti in tal caso (e solo in tal caso) la conica impropria è non degenere immaginaria.

Più complicato è il caso del cilindro, perché allora la conica impropria è degenere. Allora si può vedere se il minore M11 (o M22, o M33) è definito o no: le conclusioni sono le stesse; infatti M11 (per esempio) definito (positivo o negativo) ci dice che la conica intersezione del cilindro con il piano x=0 (il cui discriminante è proprio M11) è non degenere immaginaria, e questo può succedere solo con un cilindro immaginario. (Nota: se hai in mente un cilindro con generatrici parallele al piano x=0 che, nello spazio affine, non lo intersecano, questo NON è un controesempio, perché in realtà siamo nell'ampliamento proiettivo e le generatrici incontrano comunque il piano nel loro punto improprio).