In this work we gave a general, robust and efficient approach for dealing with numerical solution of partial differential equations (PDEs) arising in image processing and computer vision.

The well established variational computational techniques, namely finite element, finite volume and complementary volume methods,  were introduced on common base to solve nonlinear problems of image multiscale analysis. 

Such methods have strong physical background since they are based on principles like minimization of energy (finite element method) or conservation laws (finite and complemetary volume methods). They allow clear and physically meaningful derivation of  difference equations which are local and easily implemented.

The variational methods were combined with semi-implicit discretization in scale, which gives favourable stability and efficiency properties of computations.

We show here  stability without any restriction on scale steps.

Our approach lead finally to solving of linear systems in every discrete scale level which can be done efficiently by fast preconditioned iterative solvers.

We discussed such computational schemes for the regularized (in the sense of Cattè, Lions, Morell and Coll 1992)  Perona-Malik anisotropic diffusion equation (1990)

and  for nonlinear degenerate diffusion equation of  mean curvature flow type studied by Alvarez, Lions and Morel (1992).

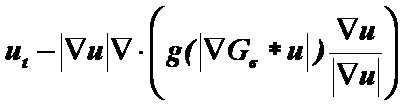
A.Handlovicova, K.Mikula, F.Sgallari, Variational numerical methods for solving nonlinear diffusion equations arising in image processing, Journal for Visual Commun. and Image Representation, Vol. 13, No.1/2 (2002) pp. 217-237

We introduce linear semi-implicit complementary volume numerical scheme for solving level set like nonlinear degenerate diffusion equations arising in image processing and curve evolution problems.

We study discretization of image selective smoothing equation of mean curvature flow type given by Alvarez, Lions and Morel (1992).

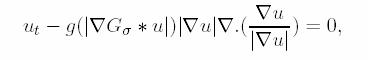
 Solution of the level set equation of Osher and Sethian (1988,1990) is also included in the study.

We prove      estimates for the proposed scheme and give existence of its (generalized) solution in every discrete time-scale step.

Efficiency of the scheme is given by its linearity and stability. Preconditioned iterative solvers are used for computing arising linear systems.

We present computational results related to image processing and plane curve evolution.  

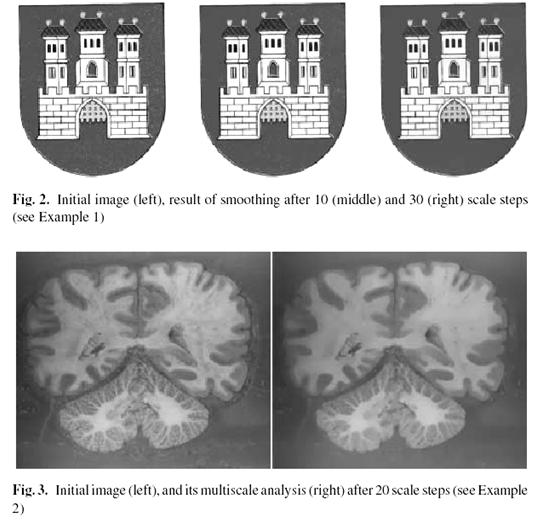
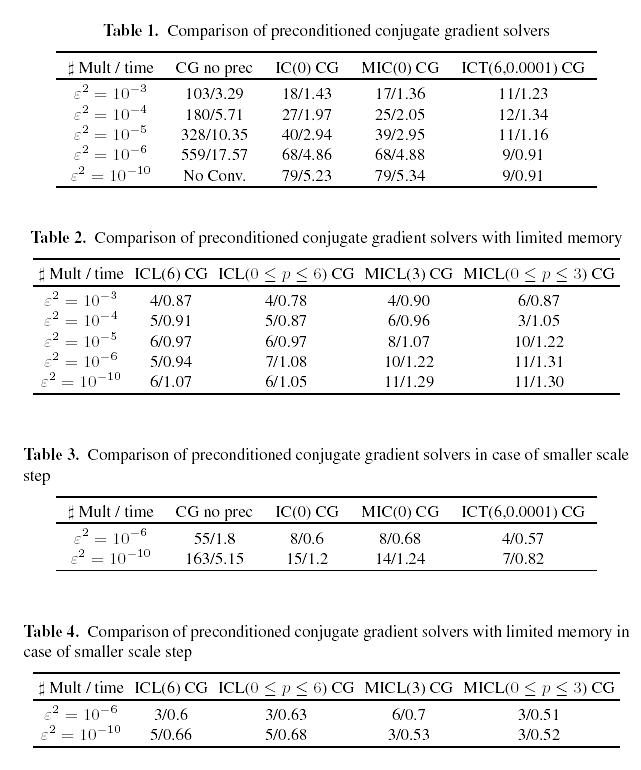
CPU time in seconds on Dgital Alpha XP 1000 workstation.

  A.Handlovicova, K.Mikula, F.Sgallari, Semi-implicit complementary volume scheme for solving level set like equations in image processing and curve evolution, Numerische Mathematik, Vol. 93, No. 4 (2003) pp. 675-695 (pdf file) (poscript file)

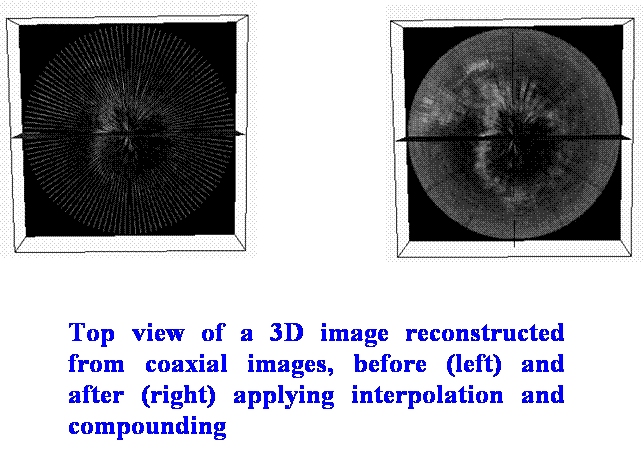
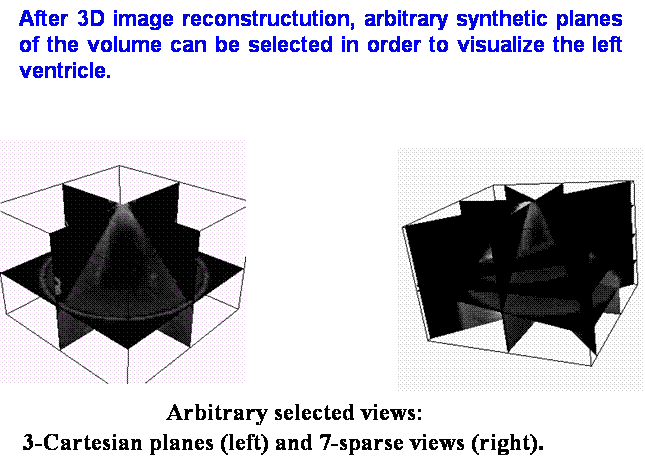
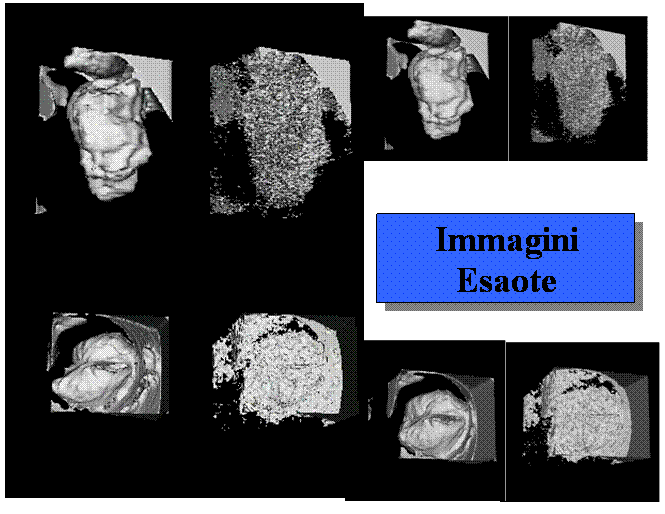
Nowadays, 3D echocardiography is a well assessed instrument in medical diagnosis, in particular low-cost echocardiographic acquizition devices scan 2D slices rotated along prescribed direction.

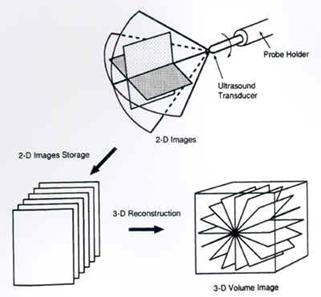
  Then the discrete 3D image information is given on cylindrical grid. Usually, this original discrete image intensity function is interpolated to uniform rectangular grid and then numerical schemes for 3D image processing operations (e.g. nonlinear smoothing) in the  uniform rectangular geometry are used. However, due to large amount of noise present in echocardiographic images, the interpolation step can yield undesirable results.

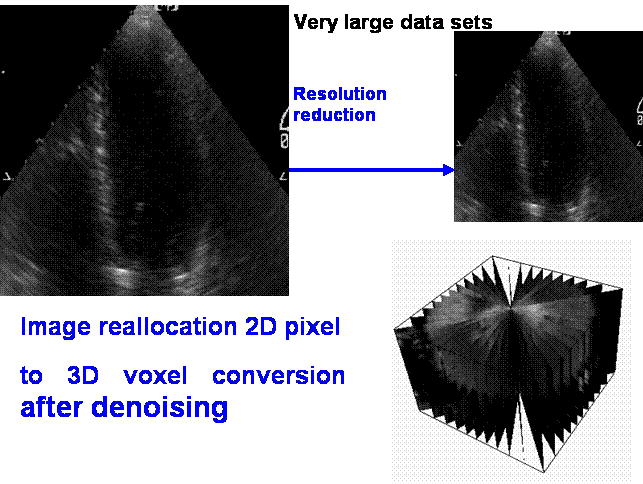
In this work, we avoid such step and suggest 3D finite volume method for image selective smoothing  directly in the cylindrical image geometry. Namely, we study semi-implicit 3D cylindrical finite volume scheme for solving Perona-Malik-type nonlinear diffusion equation and apply the scheme to 3D cylindrical echocardiographic images. The   -stability and convergence of the scheme to the weak solution of regularized Perona-Malik equation is proved.

K.Mikula, F.Sgallari, Semi-implicit finite volume scheme for image processing in 3D cylindrical geometry, Journal of Computational and Applied Mathematics , Vol. 161, No. 1 (2003) pp. 119-132 (pdf file) (poscript file)

  Return to Fiorella Sgallari's Home Page