TRIPTURES-TRITTURE

TRIPTURES

A tripture is a triple of pictures, where the last is the superimposition of the other two.

As an example, take a look at these three pictures A,B and C:

Our goal is to produce two new images A' and B' looking as A and B, such that their superimposition C' looks as C.

We get this result by producing the two images A' and B' in the next picture:

If A' and B' are printed on a transparency, the superimposition of A' and B' produces the image C'.

How to produce your own triptures

The procedure involves some steps:

• First of all you need two black and white images A and B OF THE SAME SIZE. You can reduce the number of colors in your own images to 2 by using an image editor.
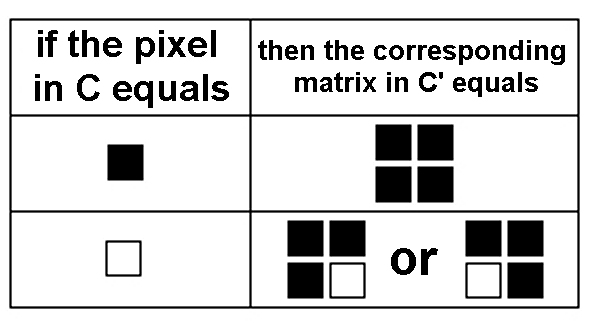
• Secondly you need to replace each pixel in A and B with a 2x2 square matrix (you can do that, e.g., by using MATLAB or MATHEMATICA). Follow these rules: E.g., if the pixel in A is white, we replace it with the matrix having black pixels in the cells (1,2) and (2,1) and white pixels in the other two cells. If the pixel in B is white and the corresponding pixel in C is black, we replace it with the matrix having black pixels in the cells (1,1) and (2,2) and white pixels in the other two cells. Note that the replacement in B takes the image C into account, contrary to what happens for A.
• After the previous replacement we get the wanted images. However, our rules are asymmetrical, since only B' contains the information about C. This fact produces some kind of unpleasant regularity in A'. Indeed, the pixel corresponding to the cell (2,1) (i.e. row 2, column 1) is always black. In order to eliminate this problem it is advisable to exchange, with probability 1/2, the colors of the two lower pixels in the corresponding 2x2 square matrix of A' considered in the previous step. Then, if those colors have been exchanged, we do the same for the lower pixels in the HOMOLOGOUS 2x2 matrix in B'.

NOTE: if the size of A and B is mxn, the size of A' and B' is 2mx2n.

If you use MATLAB and you are content with a rough m-file, you can download this m-file to produce your own tripture. Just rename your images A and B to image1.jpg and image2.jpg, respectively. The m-file will produce the files newimage1.jpg and newimage2.jpg, representing A' and B'. Their superimposition will show C'.

Some advice to produce a good tripture:

• In order to see the image C', it is necessary that the images A' and B' are PERFECTLY superimposed. I suggest to print A' and B' by using a good printer and to use the option "Print Corner Crop Marks". This will allow you to get a perfect superimposition.
• Although this method can be theoretically applied to images A, B and C of any dimension, too large images make a perfect superimposition too difficult to obtain. If you have a normal laser printer for A4 paper just use 200x300 images or kind of.
• After getting the images A' and B', printing them on two transparencies and superimposing them carefully, I suggest to staple these two transparencies together on one end and put them onto a white background.
• I have used triptures to make Christmas cards on transparencies. If you wish to make something similar, remember that when you open the card the turned page looks mirrored. You have to keep this in mind when you make your tripture.

How does this method work?

This method works because if we apply the previous rules we get that

In other words darker pixels in C correspond to darker 2x2 matrixes in C', while lighter pixels in C correspond to lighter 2x2 matrixes in C'. Let us examine this fact more carefully. In each 2x2 matrix of A' the information concerning A is represented by the pixel (1,1), while the pixel (1,2) is always black. Analogously, in each 2x2 matrix of B' the information regarding B is represented by the pixel (1,2), while the pixel (1,1) is always black. Therefore in the superimposition of A' and B' the pixel (1,2) of A' hides the pixel (1,2) of B', and the pixel (1,1) of B' hides the pixel (1,1) of A'. In other words the pictures A and B hide each other in C'. The information concerning C is contained in the second row of each 2x2 matrix in C'. Each white pixel in C corresponds to setting two different colors in that second row, while each black pixel in C produces two black pixels in that second row.

I hope you will have fun in making your own triptures!

---

P.S: I have developed this technique to produce my Christmas cards, but I have later discovered that it was already known in the scientific community. Please inform me if you know some similar or better procedure to get an image by superimposition of other two.

This is my email address: